71@Asish.. So what is the final solution of yours?
Which of the following forces are conservative in nature?
a. F = a\hat{i} + b\hat{j}
b. F= ax\hat{i} + by\hat{j} \,\,\, (a\ne b)
c. F= xy\hat{i}
d. F= x{^2}y\hat{i} + 2xy^{2}\hat{j}
-
UP 0 DOWN 0 0 21
21 Answers
49@ Ashis: i read up wiki....and understood this... i am writing that here:
A vector field 
is said to be conservative if there exists a scalar field 
such that
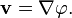
Here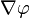 
denotes the gradient of . When the above equation holds, is called a scalar potential for .
The fundamental theorem of vector calculus states that any vector field can be expressed as the sum of a conservative vector field and a solenoidal field.
well...that is what i said...
here is the scalar potential at a point
is the field
thus,
(any path)P∫ν.dx=φ(x1) - φ(x2)
i.e.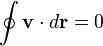 
x is not the cartesian x coordinate but gives position of particle....
and this is what i was telling for so long!!!! :P
106Euclid is correct ... (just go look up curl in wiki) ..
you can simply apply what he has written and if it indeed turns out to be zero then the force is conservative
11Can't you see I wrote your name there, but kya kare tum apni rone ki aadat se kabhi baaz
nahi aaoge.:P :P
What is ROFL?
71Tab toh mera kaam aasan ho gaya. ROFL!
Nai Nai! Seriously... It takes much long time to complete. But If you are talking about genie Subho then I agree with you!! :P
71'Nabla' is an operator.
Like + adds two things, It is also an operator which has many uses.
Extracts from Wikipedia
"When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus. When applied to a field (a function defined on a multi-dimensional domain), del may denote the gradient (slope) of a scalar field, the divergence of a vector field, or the curl (rotational) of a vector field, depending on the way it is applied."
@khyati.. Calculus.. Woh kya hota hai. Mujhe abi kuch nai pata usme. :)
23a , b are conservative ,
c is not conservative
see basic idea is
if u can find ∫Fxdx + ∫Fydy without using the relation between x and y , then the force F is conservative
eg: F = xy2i + yx2j
then ∫Fxdx + ∫Fydy = ∫ xy2dx+∫yx2dy
= ∫d(x2y2)/2 = x2y2/2
there was no need of any relation between x and y , hence it is conservative
try same for option d
49well the nabla can be found out by partial differentiation techniques..
in partial differentiation, there are more than one independent variables like x y and z and when we differentiate w.r.t. x we consider the other variables to be constant...
49well what i say and what u say imply the same
E.dl if u look carefully can be used as a measure of potential at that point...
and now....
If w.r.t. any path taken ∫E.dl is same for any two points then, we can assume a fixed value of potential assigned to each point and the potential difference between the two points is the difference between the two points....irrespective to the path...
so E.dl summation over a closed path gives the difference between the same value which is zero....
and @ Euclid... i do not think that u are quite right...
23@ subhomoy
wat i hav said is correct
check the basics, wat u r telling by stating ∫E.dl=0 in a closed path , is not a sufficient condition .
When work done by a force is " independent of the path taken " then it is called as a conservative one .
When writing ∫E.dl viz ∫Exdx+∫Eydy
if u get the integral without knowing the relation between x and y , it simply means that the work done is independent of the path taken .
but if u reqd the relation between x and y , it means that work done IS NOT independent of the path taken
1If \vec{\bigtriangledown } \times \vec{F} = \vec{0}, then the force is said to be CONSERVATIVE.......
where \vec{\bigtriangledown } \rightarrow differential operator, given by
\bigtriangledown = (\frac{\delta }{\delta x}\hat{i}+ \frac{\delta }{\delta y}\hat{j}+ \frac{\delta }{\delta z}\hat{k})
49actually no....
a conservative field is given by
summation of (field.dl) = 0
just apply that taking any arbitrary closed loop like circle square triangle and that solves the problem....