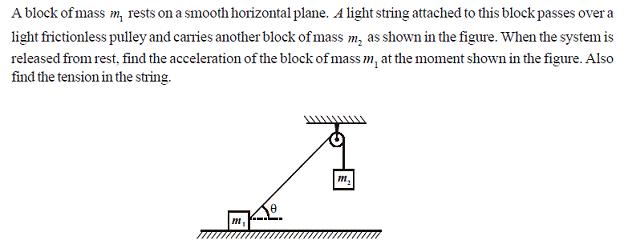
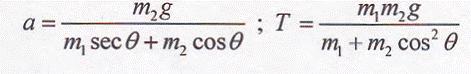1
1An ATTEMPT:
At the particular given instant ... the system can be considered to be momentarily at rest ... The tension in the string can be broken in sine and cosine components ... Tcosθ moves the m1 block [ friction not present ]. Tsinθ balances the weight m1g
Hence Tsinθ = m1g ..... (1)
Now on m2 block .... T = m2g .... (2)
Hence .. by solving sinθ = m1m2
Now considering acceleration of block m1 ...
Since T = m2g ... from (2) ...
Tcosθ/m1 provides the acceleration of the block m1
m2gcosθm1 = reqd. acceleration ...
cosθ = √(1 - sin2θ) = √(m22 - m12)m2
Hence the reqd. soln... is g√(m22 - m12)m1
 1
1ans given is---
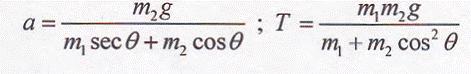
by putting the value of theta ans. doesn'y comes same as this
 23
23arka ur solution is not correct .
sinθ =m1/m2
implies θ = constant wich isnt true
 1
1yeah....
if u take vel. of m1 as u nd that of m2 as v u will get a relation
v= u cos (theta).....
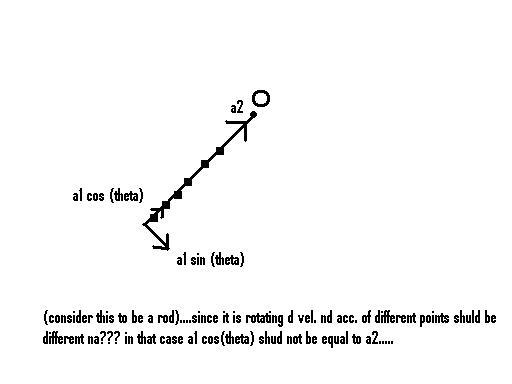
but d problem is that we cannot take the same relation for their acceleration.....since it has a rotational component as well....
 6
6i think normal reaction also has to be included...
 23
23\vec{a_{1}}=a_{1}cos\theta (\hat{t)}+a_{1}sin\theta (\hat{n})
\vec{a_{2}}=-a_{2}(\hat{j})
where \hat{t}=unit vector along the string
and \hat{n}=unit vector perpendicular to string
now since string is inextensible and it doesnt slack , acceleration of both ends of the strings along the string shud be equal .
hence a1cosθ = a2
m2g-T=m2a2=m2a1cosθ
Tcosθ=m1a1
thus m2gcosθ=m1a1+m2a1cos2θ
hence 
 1
1Ya ... I got it ... I considered a case in which θ is always constant ...
 1
1i hv little doubt in this.....
 1
1plz dp reply.........................