Somebody help me!!
In the given arrangement pulley P1 and P2 are moving with constant speed vo downward and the centre of the pulley P lies on the principal axis of a convex mirror having radius of curvature R. Find the speed of image of pulley P when it is at a distance x from the surface of convex mirror in terms of vo, R, x and θ
I am stuck up in finding the velocity of the pulley P3.
Here is my attempt-
Let xo and xp be the distances of Pulley P1/P2 and Pulley P3 from the support at any instant.
I used constraint relations to obtain-
2xo + 2xpcosΦ + 2xo = Total length of the string,
Now considering the change in lengths and differentiating,
4vo + 2vpcosΦ - 2xpsinΦ = 0
so that vp= (2vo + xpsinΦ)/cosΦ
At the instant given, vp= (2vo + xpsinθ)/cosθ,
According to the solution, v = 2vo/cosθ
Can somebody find out my mistake?
Any help appreciated
-
UP 0 DOWN 0 0 9

9 Answers
4xo + 2xpcosΦ = L
If we differentiate
4vo + 2vpcosΦ - 2xpsinΦ = 0
Both Φ and xp are variables.
Whats wrong?
If v is the vel of the P3
then we would have,
v cosθ = 2vo
then evrythng follows!!
i will give my theory...as i am no-so-good at finding mistakes...
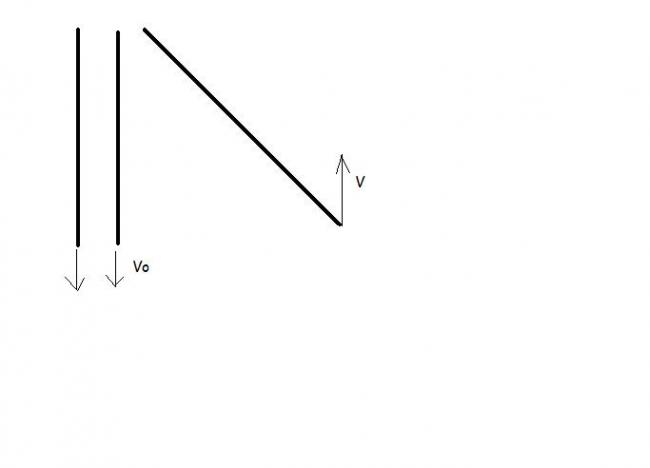
so the pulley P1 elongates the string length by 2vo whilst the pulley P3 shortens it by vcosθ
since string length is const in this 1 sec,
2vo-vcosθ=0
giving relation..
same relation for the other pulley also! :)
the figure of the problem is here:
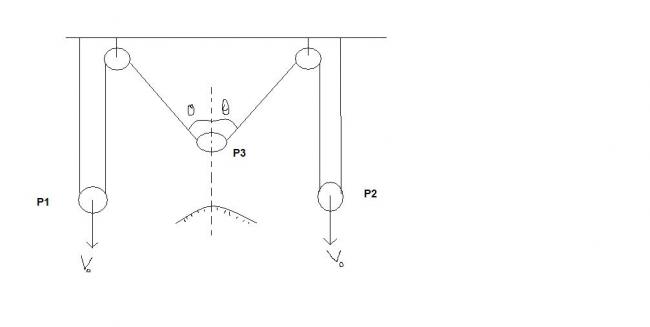
(provided by swordfish! I wonder why he calls himself so! )
Thanks for your time ATGS!
Even I got the same as you told...2vo=vcosθ by simply looking at the figure.
This time I was interested in doing through fundamentals so gave it a try [1] but failed [2]
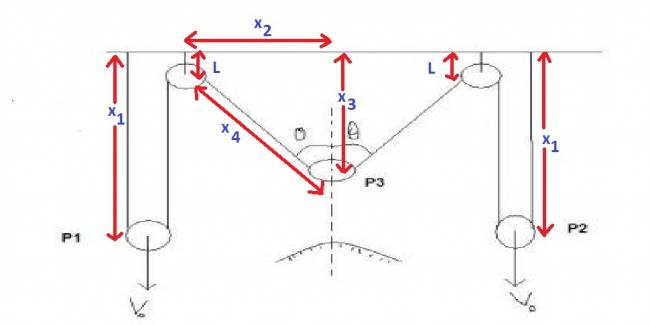
2(2x1-L)+2x4 = const
i.e 2x1 +x4= const
so 2v1+v4 = 0
x42= x22 + x32
x4v4=x3v3
x3=x4cosθ
so v4=v3cosθ
so 2v1+v3cosθ = 0