9dx/dt = u - vsinθ
dy/dt = - vcosθ ....................1
x = y tanθ
solving
y = L(1+sinθ / cosθ )-v/u ..........2
solving 1 and 2
T = Lv / (v2 - u2 )
is this the ans ?
Point A moves uniformly with velocity 'v' so that the vector 'v' is continually "aimed" at point B which in its turn moves rectilinearly and uniformly with velocity u<v. At the initial moment of time v perpendicular to u and the points are separated by a distance l. How soon will the points converge?
-
UP 0 DOWN 0 5 16
16 Answers
9
1yeh the answer is right.. but jumped a lot of necessary steps but thats alright
9Riju tell me if u r not getting the skipped steps
i can type them if u want
66The following is my version of solution. Just replace the word "ship" with "particle" ( I actually answered in another context, I am just copying that solution)
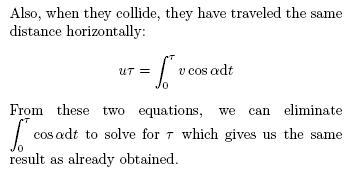
1How are u obtaining 0=-(v2 - u2)\small \tau + vl
Are u substracting the first from the second equation?
66Because when they collide, A, B, C are becoming the same point, so AB=0 and BC=0. So the LHS = 0.
62Kaymant sir, I am waiting for your book.
I would really love to read it.
The alternative solution though is fairly well known, I was more impressed with the first solution :)
1Kaymant sir is a treasure to this forum..., as said by nishant bhaiyya, the second one was regulation, in all buks like irodov soln.s, arihant and all..., but the first one was really gud..., even ill await ur buk sir...
1see , this site is a base of students to clear their concepts....u shud join here rather than doing orkutting
1i tried to do this sum on my own and found a new solution (well not exactly new)
l=vsin@dt (integrating form v to t1 ) as the toal perepndicualr distance will be t1
and
ut1=vcos@dt (integrating from v to t1)
but my problem is that i cant solve it mathematically .....
someone pls help this great novel idea into coming into life :)
1nyc question budddy.....................buh u rock i forgot to tell ya ...u noe.......u rock!!!! well thw ans is::: dunno yaar i wish i had joined iit buh u noe i m a funk so c to it ........join da club........