someone helppppppp
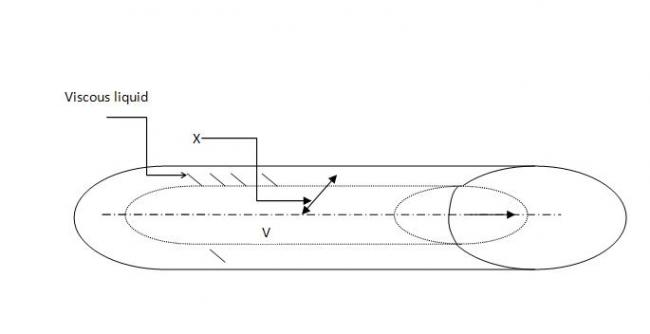
A long cylinder of radius R is displaced along its axis with constant velocity u inside a stationary co-axial cylinder of radius r.The space between cylinders is filled with viscous liquid.Find the velocity of liquid as a function of distance x from the axis of cylinde.Assume flow to be laminar
-
UP 0 DOWN 0 1 8

8 Answers
try this
take a thin cyllinder of radius r of thickness dr
velocity at lower surface is vr and at upper surface is vr+dr
now the force acting on ti will be P.2pi.r.dr (P is the pressure difference at the ends of the cyllinder)
balance the viscous force in these two ways..
this will give the solution..
the other side of the force will be by integrating
2.pi.(r+dr).ηdv(r+dr)/dr - 2.pi.r.ηdv(r)/dr
sir cant reach to the answer,maybe some mistake in my solution................if u have done so,kindly give the solution.......
answer given in book is 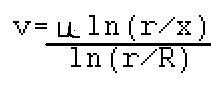
equating the two things i gave...
L{2.pi.(x+dx).ηdv(x+dx)/dr - 2.pi.x.ηdv(x)/dr} = P.2pi.x.dx
So,
(x+dx).ηdv(x+dx)/dx - x.ηdv(x)/dx = P/L.x.dx
so,
η.d/dx(x.dv/dx) = P.x.dx / (Lη)
integrating we get
x.dv/dx=P/(Lη)x2/2+c
dv/dx = P/(Lη).x/2 + c/x
again integrate to get
v=P/(Lη).x2/4+cln.x+c1
put x=r, v=0
x=R, v=u
this will give u value of c and c1 the two constants of integration