17 monthss ho gaye bhaii koi toh karo:P:D
Consider the infinitely tall system of identical massive cylinders and massless
planks shown in Fig. The moment of inertia of the cylinders is I =
MR2/2. There are two cylinders at each level, and the number of levels is
infinite. The cylinders do not slip with respect to the planks, but the bottom
plank is free to slide on a table. If you pull on the bottom plank so that it
accelerates horizontally with acceleration a, what is the horizontal acceleration
of the bottom row of cylinders?
-
UP 0 DOWN 0 0 19
19 Answers
21ok see this for its soln- http://bit.ly/9KML0k
u can get upto the recurrence relations but after that its something abt eigen values and vectors as philip said...
49
so this is it...i am thinking ki the mid has forward acceleration a' and angular acceleration in anticlockwise direction as α...
the lower nth planck has acceleration as an and higher planck has acceleration as an+1
49ok so din post any more yesterday coz this approach led me to no where....so i am thinking of a new approach!![4][4]
49so, when n th planck is set into acceleration, the planck wants to remain in its position by virtue of its inertia...
lets take this problem to non inertial levels...LOL
so the cylinder faces a pseudo force of manLOL..MAN!!
this force wants to slide the cylinder and invites friction in the opposite from both the nth and (n+1)th planck...
49
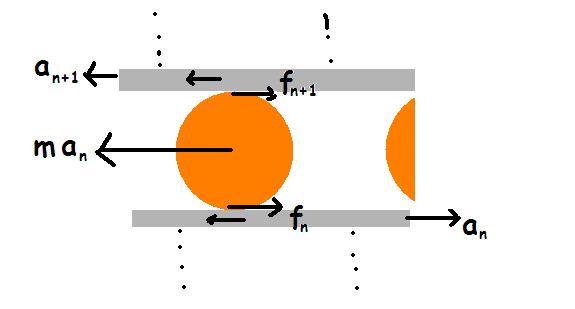
i am representing the n th planck and n+ 1 th planck from base..
49lol...:P:P
arre yaar mujhe abhi tak wahi wala answer jo maine diya tha correct lag raha hai!!donno!!!!
21i guess this q is not solvable by jus using the concepts within the jee syllab.....it involves i guess some concepts which arent in jee syllab.......
49but i still thnk we can just ignore the other things xcpt the 1st row of balls since none of the forces give the torque or force in direction of motion of propagation except friction......but friction on top is μ*(wt of lowest sphere) less than that in the bottom......
1i could not find anything in that book to help us any further ??
1I think we can solve till the recurrence relations
I wasn't able to get any headway after that
Morever the solution I saw then (long time back) was something about eigen values and vectors and stuff which went right over my head.
Maybe someone can come up with some simple solution ?
49try out.....seems to be easy.....if not we'll see again........targetiit to hai na........koi na koi hlp jaroor karega...
49according to me there is no significance of the tower........due to absence of tangential forces.......just apply pseudo force and condition for pure rolling.....i think dat will help....