but ans toh D hai... wahi toh confusion hai :"(
10 Answers
shouldnt it be b?
Or am i missing something very important?
<pre lang="eq.latex">
\documentclass{article}
\begin{document}
Hello World!
\end{document}
</pre>
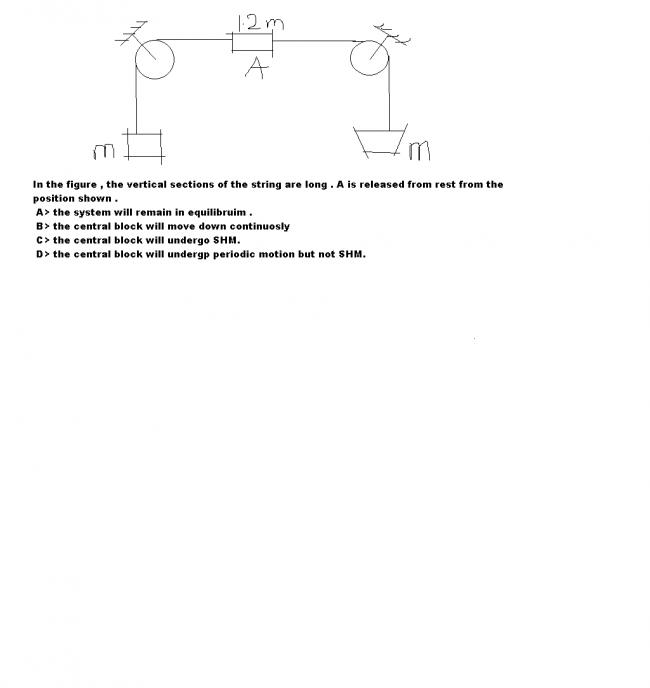
common sense that net force = 12mg downward so it will always move downward... but then i thought maybe the T will be greater than 12mg then.... but i proved that it wont
method 1
i think (b) too. consider at any angle when the string makes angle θ with the vertical...
Let acceleration of 12mg be a(downward) then acceleration of the two masses m will be asecθ upward due to constraint relation.
Writing force equation for 12m....
12mg - 2Tcosθ = 12ma .... (i)
force equation for m...
T-mg = m.(asecθ) .... (ii)
Solving them for a, we get a=mg(6-cosθ)/7 which is always positive hence acceleration is always downwards ... no chance of coming to equilibrium even..
method 2
the body has a possibility to move up if the system remains at equilibrium at some point.... but at no position u can make the body at equilibrium... hence it cant move up...
yaar ye 1.2 hai how will i know! :D
okie.. then the answer will be D
:O
wo kaise likhe...
\int_{0}^{1}\frac{x^{4}\left(1-x\right)^{4}}{1+x^{2}}dx
=\frac{22}{7}-\pi
ye wala..
ispar bhi kaam chal raha hai kya...labs me :P
image uploader ki tarah ye bhi baad me public hoga... [7][1]
if it is 1.2m then...
for mean position.
2Tcosθ=1.2mg .... (i) [θ is angle made by string with vertical]
T=mg .... (ii)
from (i) and (ii),
cosθ=0.6=y/√a2+y2
==> y=3a/4
Any disp. x below the mean position
2Tcosθ - 1.2mg = 1.2ma.... (iii)
by constraint relation, acceleration of block of mass m is asecθ
So, mg-T=masecθ ..... (iv)
Finding the value of a,
a = (5cosθ - 3)/8
now, cosθ = (x+y)/√(x+y)2+a2
now putting y=3a/4,
cosθ=z (say)
putting value of cosθ we dont get a is directly proportional to x but it will definitely be periodic as we can find an equilibrium position.
@priyam woh latex hai?? bhaiyya will u be introducing latex?? accha hoga.