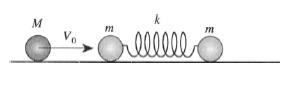
1The velocity of COM = V22 = V4 ........( let )
Now , the kinetic energy of the balls must be converted totally into the potential energy of the spring after everything has stopped : )
So , 12 K A 2 = 12 m V42
Or , A = V0 Mω ( M + m )
Now , the motion of the ball 2 can be completely described as : -
x2 ( t ) = x2 ( t ) [ In COM frame ] + xCOM ( t )
= V0 Mω ( M + m ) sin ( ω t ) + V0 M tM + m
= V0 M tM + m [ 1 + sin ( ω t )ω t ]
whereas , ........ x1 ( t ) = V0 t ( M - mM + m )
For collision to occur between balls 1 and 2 , we obviously need to have
x1 = x2
1
Ricky
·2011-03-21 02:08:38
Sir ,
Mm = - sin xx = ξ ...............( 1 )
How is -
M = mξ Min. ?
Later , I found out the mistake -
mM = - sin xx ...................instead of ( 1 )
Thanks Sir .
66Once you get the equation
sin x x= - ξ
and you are looking for the min of ξ so that a solution may exist, just look for the absolute minimum of the function sin xx. This is easier said than done.
One way is to differentiate w.r.t. x and equate the derivative to zero. This gives the transcendental equation
tan x = -x.
There is no algebraic solution, but graphical means give x ≈ 2.02875 (which is very roughly 2/3π).
From here we get M = m/ξmin ≈ 10 kg. (This again you taken wrongly, ricky. You found M = m ξmin which won't be 10kg)
1
Ricky
·2011-03-21 00:38:01
" But your assertion that the min is 2/3Ï€ is not correct. "
What is the reason behind this , Sir ? : )
66
kaymant
·2011-03-20 23:28:55
Well yes, I overlooked the interval you specified (and the last statement was a blind guess).
But your assertion that the min is 2/3Ï€ is not correct. If you see the answer I gave was only approximate.
1
Ricky
·2011-03-20 23:12:17
No Sir , Not at all . In fact , please google " Jordan's Inequality " sir , I think that's enough .
66
kaymant
·2011-03-20 23:07:08
@Ricky, check your inequality again. How do you get
sin xx ≥ 2π
That's true for the integral of sin x/x
1fantastic work ricky......
& an excellent ques from anant sir,,,
1
Ricky
·2011-03-20 12:15:28
EDIT - POST NUMBER 10 : LINE NUMBER 5 SHOULD BE READ AS : -
M V02 = M V12 + m V22
1
Ricky
·2011-03-20 12:09:11
Since the equality holds true in the second inequality if and only if -
x = 3 π2 , i . e ,
ω t = 3 π2
Hence the required time elapsed between the collisions = 3 Ï€2 √ m√ K = 3 Ï€ √ m√ 8 k ≈ 5 seconds ........if my calculator is right : )
1
Ricky
·2011-03-20 12:03:25
Cancelling appropriate terms , we obtain -
Mm = - sin ( ω t )ω t = ξ ......... ( let )
Now we need to minimise " ξ " .
Jordan ' s inequality states that , for any " x E ( 0 , π2 ) " ;
sin xx ≥ 2π
Just changing the interval suitably , we can derive the following : - For any " x E ( π , 3 π2 ) " ;
- sin xx ≥ 23 π
Hence , ξ Min. = 23 π
Consequently , M = m ξ Min. = 2 m3 π ≈ 10 Kg
66
kaymant
·2010-05-25 23:27:11
approach is okay... however the graphs are not the ones you are looking for......
and
M\approx \dfrac{2}{3\pi}m
1
Ricky
·2011-03-20 11:23:52
Here , ω = √ K √ m , where " K = New spring constant " .
Immediately , one would ask , " why is there a new spring constant " ? It is because the effective length of the spring has been halved in COM frame . Accordingly , since the spring constant is inversely proportional to the length of the spring , hence ,
K = 2 k
Now the quest is to find the amplitude .
1
Ricky
·2011-03-20 11:16:03
Let V1 and V2 be the velocities of the respective balls ( 1 and 2 ) after the first collision .
Of course , after the first collision , the speeds of balls 2 and 3 must be equal .
Momentum and energy conservation gives us -
M V0 = m V2 + M V1
M V02 = m V22 + M V02 )
Easily solving for the assumed velocities , we find -
V1 = V0 ( M - mM + m )
V2 = V0 ( 2 MM + m )
If we now fix the reference frame to the center of mass of the two connected balls , it is easy to realize that the masses are just contracting and expanding in that frame , i . e , they are performing S . H . M .
Now , it has to be noted that the equation of the S . H . M . has to be a " sine " curve , since , at " t = 0 " , there was no S . H . M .
Let the equation of the motion with respect to COM be - x ( t ) = A sin ( ω t )
1Hopefully not......
This one came in some olympiad maybe.....
it says (Moscow Phys-Tech) and I don't know what that means.
but its a basic one for all that....
I had thought of posting this one long time ago but seeing the interest in some other mechanics problems I posted, I thought its useless :P
66
kaymant
·2010-06-04 10:30:46
Is this going to end in the archives?
1
Ricky
·2010-05-27 06:38:03
Thanks yaar , but now how to proceed ?
1
Ricky
·2010-05-27 05:58:23
I am really very sorry if I hurt your emotions , very sorry . But in fact , I just wanted to know how to bring in that " sin x " , that ' s all . I know that it ' ll execute SHM with a reduced mass frequency , but where does " sin x " come in ? Please , this is my doubt .
I am weak in Physics [2][2] , so again sorry if I hurt you .
1
Ricky
·2010-05-26 20:19:40
@aitday , can you please tell me where does " sin x " come in at all ? All I got was ,
V0 2 { M - m m } = K x 2m + 2 V 1 ( V 1 - V 0 )
where V 1 is the velocity of the first block .
Kaymant sir , can you please give a hint ? What is the condition we have to use here ?
1aitday,will u never post the answer for the question asked??
1
terror s
·2010-05-25 23:48:53
can u post the solution sir?
