doubt mechanicss

is the answer

2v₀/[l cos(theta)]

You have found the w at the given instant.We need to find it after collision.

guyzz m not having the answer a frnd of mine gave it to me......

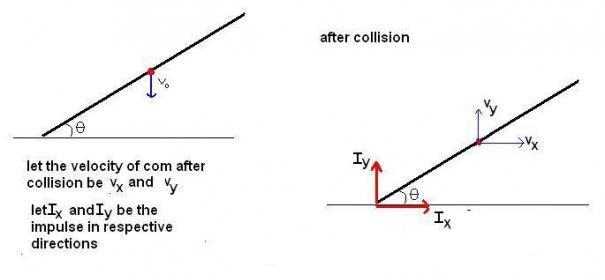
I_y = m (v_y + v_o) ........(1)

I_x=mv_x..........(2)

also
writing angular impulse abt com

I_yLcosθ2 - I_xLsinθ2 = mL²12w...........(3)

since collision is elastic , energy is conserved

mv_o²2= mv_c²2+ 12I_cw² = m(v_x²+v_y²)2 + 12I_cw² .........(4)

now since friction isnt present I_x= 0 ...........(5)

now unknowns are v_x ,v_y,I_x,I_y, w
i.e 5 unknowns and we hav 5 eqns

so u can find w

( i m not sure abt the 5th equation , experts pls confirm )

yaar qwerty ek baat bata collision ke just dt second ke doraan uske pas x me velocity kaise aa sakti hai.

VELOCITY CANT BE CHANGED INSTANTANEOUSLY.

At one end you say the reaction force in X is 0 and on the other hand you also considering V_cm in X.

And according to me iss question me to force ke chakkar me parna hi nahi chahiye.

BUT IF YOU DO FIND SOME MISTAKE IN MY LOGIC PLEASE DO TELL ME.

see initially i assumed both I_x and v_x

abhi agar I_x zero hota hai to v_x bhi apne aap automatically zero ho jaega,see equation 2

and after dt time , velocity is imparted by the impulse itself

and see, u cant just write the torque equation about that lowest point as Iα ,
i will tell u why

see angular momentum of a rigid system about any point P can be written as (angular momentum about P due to pure translational motion of centre of mass ) + (angular momentum due to pure rotational motion of COM abt P )

i.e
L_{p}=L_{cm,about P(trans)}+L_{cm,about P(rot)}
i.e
L_{p}=I_{cm}\omega +\vec{r}_{c/p}\times m\vec{v}_{c}

for this sum , pt P is the lowest pt of the rod so distance between COM and P remains same

differentiate both sides wrt time
\tau _{p}=I_{cm}\alpha +\vec{r}_{c/p}\times m\vec{a}_{c}

\tau _{p}=I_{cm}\alpha +\vec{r}_{c/p}\times m(\vec{a}_{c/p}+\vec{a}_{p})

\tau _{p}=I_{cm}\alpha +(\vec{r}_{c/p}\times m\vec{a}_{c/p}+\vec{r}_{c/p}\times m\vec{a}_{p})

now cross product of component of a_c/p parallel to r_c/p will be
zero, and component of ac/p perpendicular to r_c/p is simply r_c/pα

so \vec{r}_{c/p}\times m\vec{a}_{c/p} = mr^{2}_{c/p}\alpha

so

\tau _{p}=(I_{cm} +m{r}_{c/p}^{2})\alpha +\vec{r}_{c/p}\times m\vec{a}_{p}
\tau _{p}=I_{p}\alpha+\vec{r}_{c/p}\times m\vec{a}_{p}

here since pt P is accelerated u cant just simply write torque abt P = I_pα

second term me woh extra term kyo hai .

us to a-@r likh diya hai

Hey guys....
Can't we proceed this way?

Conserving angular momentum about the point of rotation,
mvlcosÏ‘ = ml²w/3 + mVl/2

Since collision is perfectly elastic, kinetic energy is conserved.
mv²/2 = (ml²w/3 + mV²)/2

Solving both we get a quadratic equation in w

experts n e views ?

i ve not seen the soln yet ..ll revise the chap again nd then ll try myslf nd then go through the soln btw thnxx qwerty bhaiiya nd all otherss....experts can also give their views...

wat is the difference ??

ok ok...