block A of mass 1kg resting on a horizontal surface is attached to block B of mass 0.5kg by means of a massless and inextensible string going over a frictionless fixed pulley .the string connected to A is loose .When B falls through a height .98m ,the string becomes taut.Find the time interval between the string becoming taut.and the instant when block A again makes contact with the horizontal surface.Also find the fraction of the kinetic energy of block A lost when it is jerked into the motion.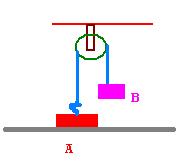
106(i) use WE principle first.
find the velocity of B just before string becomes taut.
(ii) then use conservation of momentum
i.e. -m(B)*v = m(A)*v' + m(B)*v'
where v = velocity of B before jerk
v' = common velocity after jerk
(iii) now, it is just like an atwood machine, hence accn. of A = g/3
(iv) use kinematic equation to find out time taken to reach back.
i.e. t=2*v'/(g/3)
3can u explain y the two bodies shud attain a common velocity when they are taut
can the mass A go upwards
106see, when there is jerk, analyse the fbd's of A and B for the small time interval dt.
FOR A:
there is T upwards and mg downwards. but the jerk force is instantaneous and will have an extremely high magnitude (which is exerted by the tension) hence mg will be negligible. But after the jerk it will be like an atwood machine.
FOR B:
Again there is the jerk so, u can see both will go up and from constraint relations they will have common velocity.
There is a similar example in HC VERMA (last example of conservation of momentum)
btw: is the answer coming correct?
3yes asish u r rite with the approach.i didnt think abt the strength of the jerk force .
106no, subash both will have upward velocity immediately after jerk.
as i said analyse the fbd of B and u will know the reason why. :)
1how can you apply conservation of linear momentum........ net force is not zero
106the reason behind conserving momentum is that the forces that come into play during that interval are so large that the external force due to gravity becomes negligibly small. see post #4 and try to solve the question which doesn't use momentum conservation.
3as soon as string becomes taut!!!!!
Jdt will act upwards on both blocks!!!!!!!!!!!!!!!!!
Jdt = (1)v.....................
at the time of jerk the mass B would hav gained velocity .... √2g(0.98) say = u ...........
-Jdt = (0.5)v/ - 0.5u .............
but ull see by constraint eqxns v/=v!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
solve and get v !!!!!!!!!!!!!!!!!!!!!!!
now as soon as they get velocity v there will be a deceleration on both blocks by 0.5g/1.5... hence u can calc. time also!!!!!!!!!!!!!!!!!!!!!!!!
