1ya true :) , I loved it .
Let the aspirants try , it should be some good practice for them before the exams .
2 heavy circular rollers of diameters D and d , respectively , rest on a rough horizontal plane as shown in the figure. The larger roller has a string wound around it to which a horizontal force P can be applied as shown. Assuming that the coefficient of friction μ has the same value for all the surfaces of contact , determine the necessary condition under which the large roller can be pulled over the small one .
Ans : μ ≥ √ (d/D)
This problem is from quite a popular book of engineering mechanics named Timo Shenko Young . Trust me it is just the basics , nothing more .
Let the aspirants try first .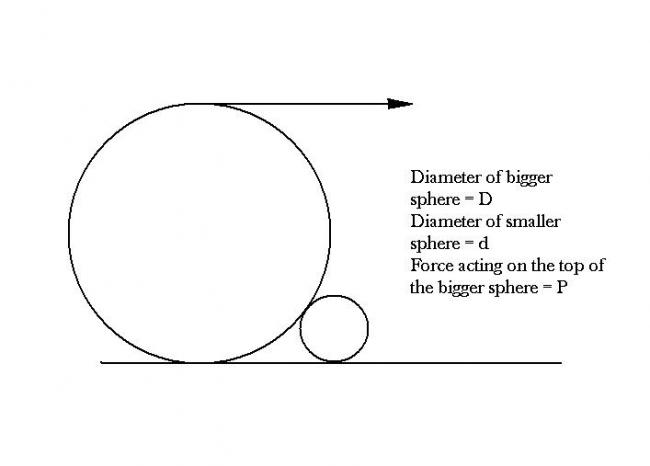 
-
UP 0 DOWN 0 5 28
28 Answers
1
1i didnt make any comment abt P
only initially friction will be maximum and at other times it will remain static ..
9i was trying keeping P constant as mentioned in q and was deriving this as impossible problem !!!
but acc to you P shud vary so that means q is wrongly framed ?
1ok so heres the solution !
consider friction at the interface between the two cylinders ..
let it be f
let the normal reaction at that surface be N
at each moment the smaller mass has to remain in equillibrium because if it isnt there will be slippin
let the friction at its ground be F to the left
then equating torques we have f=F
making the resultant of foces along horizontal 0
F+Fsinθ=Ncosθ
where θ is the angle made by the line joining the centres at any moment
but F<=μN
so μ>=cosθ/(1+sinθ)
for no slipping μ should be greater than the maximum value of the exp. right .. (so that it reamins greater throughout)
there will be different values of the right exp. for different θ but the expression is tan(π/4-θ)
so it will maximum for minimum θ which is at the intial stage ..
sinθ=R-r/(R+r) from figure
find cosθ ,..
substituting we get
μ>=√(d/D)
62hmm.. yup celestine.. there should have been friction at the bottom :)
9were is friction at ground shown in the diagram ??????????
62phew.. this is why i never wrote down anything with pen...
Good that you dared to :)
Btw the question is not as tough as it looks... It is more intimidating :)
1
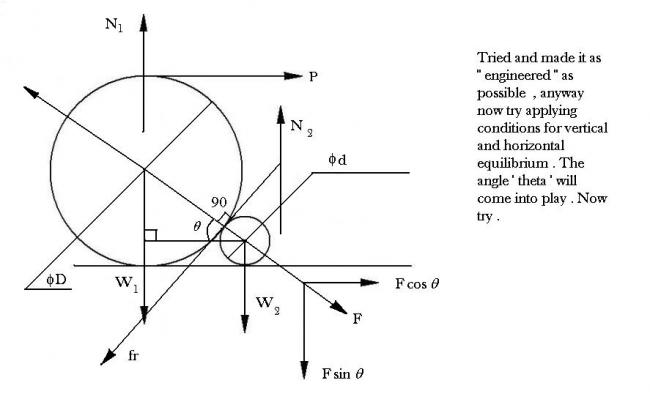
Excuse me if there are mistakes , I hope I haven't made any . Good that you tried celestine .
62celestine.. there are a few torques involved due to each of the frictional forces and the applied forces
You need to find the net torque = 0 equation..
also balance forces in each direction....
That is all i guess
what u have done on the first look seems correct :)
62well diptosh i was tempted to put the solution myself..
but din have the tempo to do it :)
but this is a wonderful question :)
9diptosh find mistake in my sol or give ur sol
no one else trying i guess
1Concepts of class - 11 ( or 12 ) only , nothing extra required .
and its not my doubt .
9till now
by considering that small roller exerts normal rn along line joining centres , got that
Ncosθ + μNsinθ ≤ P , θ angle made by line joining centre with horizontal
Nsinθ - μNcosθ ≥ Mg , M - mass of big roller
i ve assumed that smaller sphere doent move as its very heavy
i m unable to proceed further , do i need xtra info or wat concept am i missing
1ya mass is not required take frictional forces, thier torques and proceeding. in the later stage they will get eliminated.
but i am getting the answer with reverse of inequality.
1i also dun thnk os..
dats y asked...
ok if its not given dat means it si not reqd... we can take nething...
ok lemme try.. (not now :P)
is it ur doubt or u jus gave ?
1No obviously they aren't the same . Can you proceed without taking mass / weight into consideration ? I don't think so .