find the pressure at point P
1i didn't get you
3 Answers
1P=Ï(y cosθ + L sin θ)(a2+g2)1/2
where tan θ=(H-y)/(L-x)=a/g
1well its very simple. all you have to do is to calculate the depth from the free surface of water and calculate the pressure using
P=Ïa'h
where Ï=density of water
a'= resultant acceleration (resultant of a and g)
h= depth from free surface
Also, you can prove it very easily that the surface of water is always normal to the resultant acceleration (assuming hydrostatic condition) because if it would be not, then there will always be a component of acceleration along the surface of water which will disturb the hydrostatic condition.
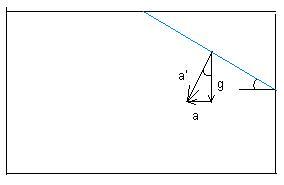
Hence tan θ=a/g
Now,
the distance from the free surface can be determined as
d=ycosθ +Lsinθ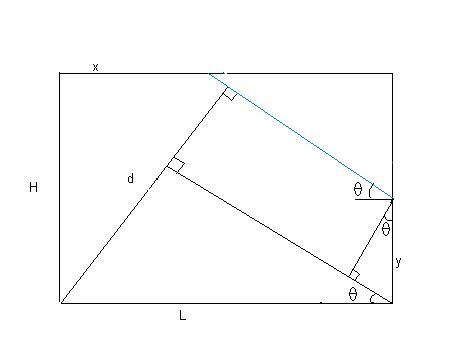
and a'=√(a2+g2