no tries!!!!!
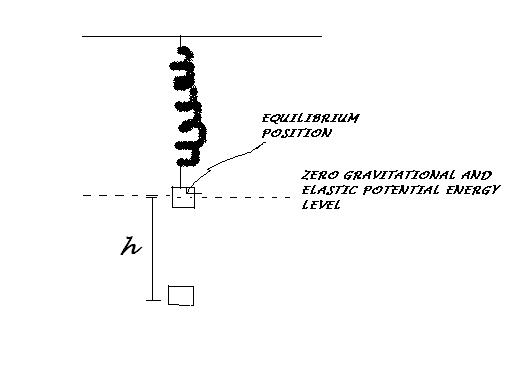
A BLOCK OF MASS M IS SUSPENDED THROUGH A SPRING OF SPRING CONSTANT K AND IS IN EQUILIBRIUM.A SHARP BLOW GIVES THE BLOCK AN INITIAL DOWNWARD VELOCITY V.HOW FAR BELOW THE EQUILIBRIUM POSITION THE BLOCK COMES TO AN INSTANTANEOUS REST!!!!
SOLUTION!!!!!!!!
[REFER FIGURE]
CHOOSE EQUILIBRIUM POSITION AS ZERO GRAVITAIONAL AND ELASTIC POTENTIAL ENERGY LEVEL
THEN AT POINT OF INSTANTANEOUS REST[SAY AT DISTANCE H BELOW]WE HAVE
1/2 MV2=-MGH+1/2 KX2
SO H=√{[1/2KX2-1/2MV2]/MG}
BUT THIS IS NOT THE RIGHT ANSWER..........CAN U FIGURE OUT MISTAKE IN THE ABOVE SOLUTION!!!!!!!!
-
UP 0 DOWN 0 1 22

22 Answers
james bond you are free to use a reference point where U=0
but keep in mind that U is a state function.... so ur energy will not be U=1/2 k x2 at any arbitrary point..
Instead it will be a more complicated expression where you have to first take the energy to the point of zero extension and then add back the energy of 1/2kx2
(A similar mistake in the applikcation of parallel axis theorem.. ) where we first have to go to the CM and then add md2 (And not directly)
sorry if i m talking nonsense!
well guys did u notice that when we derive a formula for elastic potential energy we get change in potential energy! and then we r free to choose a reference point with U=0 [1]........................hope i m being clear to all!
@kaymant sir
sorry if i m talking nonsense!!!
i got some serious basis for my saying that we can take zero pot. energy fro spring anywhere we like as i read in HCVERMA![pg-125] section 8.10 last paragraph 7th line!!!!!
Thank you sir for clarifying this
I too wasnt quite comfortable with that argument and as you said most P.E expressions are non linear.
The discrepancy in #1 was brought to clear light by akari's soln in #18
that we cannot simply write it as 1/2kx2 but instead it would be
∫k(x+x0).dx ie [1/2kx2 + mgx]
The trouble with the solution given in #1 is already resolved by Philip in #7. The reference for the spring potential energy (unlike the gravitational potential energy) CANNOT be set to zero at an arbitrary location. (But @Philip, this fact has nothing to do with the spring p.e. being nonlinear; in fact the gravitational p.e. is also non-linear.)
The potential energy is the work an external agent must do to deform it. So that means that the elastic potential energy is zero only when the spring is in its natural state. Whenever it is deformed (as in the present case), it will have some initial potential energy stored which you must take into account while conserving energy.
@jamesbond
evn i think that the correct eqn is
1/2 mv2 = mgh + 1/2 kx2 ,.......where x=h
if not
den what is the answer given ??
mathematical proof
initial situation kx0 = mg
after it decends down by say x
net force is
k(x+xo)-mg =mvdv /dx
multiply dx bth sides
(kxo. -mg).dx+kx.dx=mv.dv.....2
see the highlited thing is 0 from first equation
so wen u include wqork done by gravity u must also include the work done by initial spring force , which cancells it out
integrating 2 equation gives u the the right energy equation
@amritansh
?????????there will be no mgh term as it was already balanced by some initial extension of the spring when the system was in equilibrium ????????????
what is above statement?????how can u say so?????
don't make unclear statements like that!!!!
no the ans. is v√M/K and it comes from the eqn.
1/2 mv2 = 1/2 Kx2 where x is the distance below equilibrium u need to find
there will be no mgh term as it was already balanced by some initial extension of the spring when the system was in equilibrium
now the blow gives it a kinetic energy which gets totally converted to spring elastic potential energy
But you are disturbing the spring from zero gravitational and potential energy level , hence it should gain mgh amount of energy , not lose .
So I think the correct eqn. is 1/2 mv2 = mgh + 1/2 kx2 ,
@ anirudh, uttara............
i don't want new methods to solve the ques........i want u guys to find fault in the solution given by me!!!!!!!
what did was to use the property of SHM
using V(maximum) = Aω = A√KM=v
=> A= v√MK
@philip
we can take zero elastic potential energy anywhere we like philip.............u try deriving this result [it's too easy!!!!!!!]
ok ok
i think we cannot take the zero of the elastic potential energy anywhere we like because 12kx2 is not linear
PHILIP CAn u figure out conceptual erroe in above solution[not those petty errors of h=x [3]]
@PHILIP READ THE QUESTION......
CLEARLY SAYS WE GOTTA FIND HOW FAR BELOW EQUILIBRIUM POSITION[3]
PHILPI U R RIGHT........SO WAT'S THE ANSWER WE GET THEN!!!!!EVEN THAT IS NOT CORRECT!!!!!!
first of all be clear about what you want to find
V or X ...??
and btw that H = X