a1 is accn of m in grnd frame ,
accn of m wrt M will be a1 - a2
Please explain me the concept in this question.
Figure shows a small block of mass m kept on the left end of a larger block of mass M and length l. The system can slide on horizontal road. The system is started towards right with an initial velocity v. The friction coefficient between the road and the bigger block is μ and that between blocks is μ/2. Find the time elapsed before the smaller block separates from the bigger block.
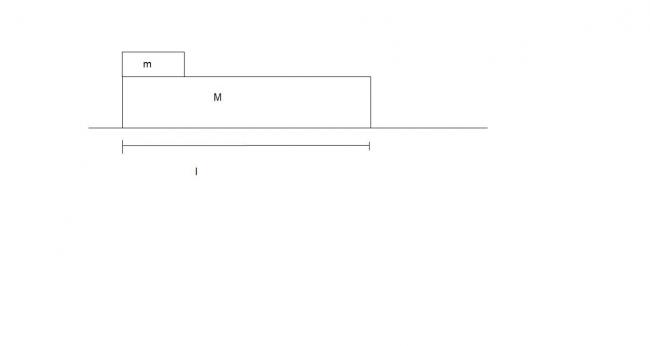
For the block M,
Ma2 = μ(M+m)g - μmg/2
a2 = Acceleration of M w.r.t. ground is μg(1+m/2M) towards right.
For the block m,
ma1 = μmg/2
a1 = acceleration of m w.r.t M is μg/2 towards right.
l = ut + 0.5a1 t2
u=0 so l = 0.5 μg/2 t2
t = (4l/μg)1/2
The answer is wrong....
Hey how is a1 w.r.t ground? I am working from the frame of reference attached on the block M, so there is a pseudo force acting on m towards right, friction towards left. Whatever accln. I find from the frame attached to M will be w.r.t to M right?
I have really doubt in this question.
The system is started towards right with an initial velocity v
How is Pseudo force acting in right then?
swordfish u hav written
"ma1 = μmg/2"
this is eqn for m in grnd frame or in M's frame ?
Errrm...may be in ground frame......
What will be its equation in the frame of M then?
One doubt...how do you find whether the given equation is from ground frame or frame of M.
@ Vivek...
Think of it this way.......The system is initially started with a velocity v ( assume no friction present....for time being)...........and then the whole system is kept on the surface where friction is present.....so there is a retardation acting on the block M.
isnt this the hcv sum?
anyways
no sawal of pseudo force here
it says the system
just remember
friction is self-adjustable
:P:P
No sawal of pseudo force?
Then what causes the smaller block to move forward and finally fall? Some kind of Devilish Force? haha
there is nothing like "pseudo force" in reality
btw swordfish it is better if u accelerations of each m in ground frame and then find relative accn of m wrt M, and then use that kinematics eqn ...
Look for the block M, its acceleration w.r.t ground will be along -i (it is decelerating)
\mu (m+M)g(-\hat{i})+\frac{\mu}{2}mg(\hat{i})=M\vec{a}
\vec{a}=\mu g\left(1+\frac{m}{2M}\right)(-\hat{i})
Now when we observe the block m from ground, it accelerates forward with
\vec{a_1}=\left(\frac{\mu}{2}\right)g(\hat{i})
Now relative acceleration of m w.r.t ground gives wrong answer.
Please help qwerty.

so m will accelerate along - ve x , ( but its accn will be less than accn of M bcz of given value of μ, hence it is able to cover that distance L )
MaM =μmg + μMg - μmg/2
so aM = μg( 1 + m2M) (-i)
am = μ2g ( -i )
am/M = μg( 1 + m2M) - μ2g ( i ) = μg2(1+mM) (i)
so
sm/M = um/M+12am/Mt2
L = 0 + μg4(1+mM)t2
t2 = 4LMμg(m+M)
I just wanted this thing-
so m will accelerate along - ve x , ( but its accn will be less than accn of M bcz of given value of μ, hence it is able to cover that distance L )
There was no need of solution. Im so sorry for wasting your time.
Thanks alot!!!