1sir...why should the total drag force depend on the length of the cylinder? shouldn't the drag force be only due to the striking of the particles onto the face of the cylinder?
12 Answers
1
1@shreyan : I think u missed the 3rd statement of the question
My soln :
Considering the differential area dS as shown.
The Volume that the area sweeps per unit time is :
2RLvcos\theta d\theta
Hence no. of collisions it suffers per unit time
2nRLvcos\theta d\theta
and therefore the average change in momentum per unit time is in the horizontal dir and is :
F=\int_{0}^{\frac{\pi }{2}}{2nRLvcos\theta d\theta (2mvcos^2\theta )} \\\Rightarrow F=nRLv^2m\int_{0}^{\frac{\pi }{2}}{4cos^3\theta d\theta } \\\Rightarrow \boxed{\frac{F}{L}=\frac{8}{3}nmRv^2}
11 acknowledgement/bibliography (whatever.. bhavanao ko samajho ) for my solution :
Nishant bhaiyya's small tip.
http://targetiit.com/iit-jee-forum/posts/area-swapped-12010.html
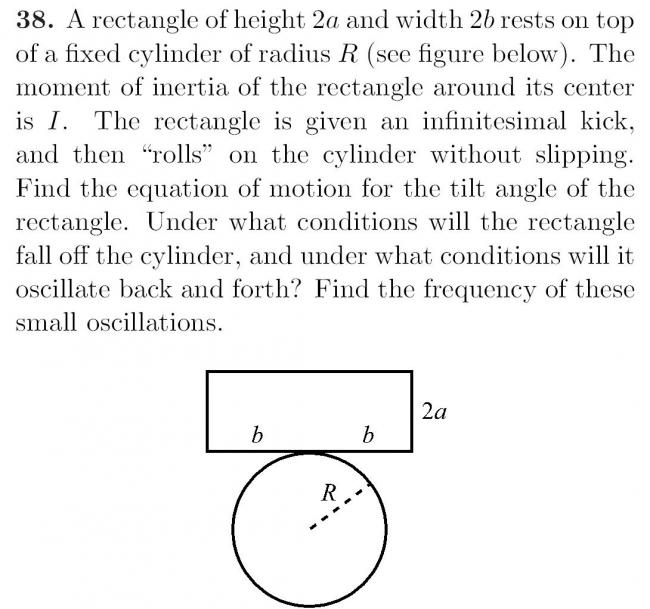
23as far as i remember ....in Q.38...the rectangle will oscillate if the new y-coordinate of COM of d rectangle due to a small displacement is greater than or equal to the y-coordinate when it is at rest as shown in fig .....
if due to d displacement .....the new y-coordinate becomes less than the older one ..then it will fall off the cylinder
2427)
Take left side extreme as origin
lets asssume that ur hand moves distance x
So its obvious that rope moves x/2
Momentum = mv =σx2v=p
From newtons law,
F=dp/dt=\frac{\sigma }{2}[v^2+v.\frac{dv}{dt}]
But V=constant
So,F=σ2v2
Length of rope =L
so hand moves 2L
=> W=F.S=σLv2
And its obvoius from the beggining that we are doing double hard work[3] to move the rope....
so energy lost=W/2=σLv2/2
23Q.38Let\; angle\; rolled\; be\; \theta
Let\; H_{i}= initial\; height\; of COM
Let\; H_{f}= final\; height\; of COM
H_{i} = 2R+a
H_{f} = R +Rcos\theta +R\theta sin\theta +acos\theta
= R + (R+a)cos\theta +R\theta^{2} \;[\theta \approx sin\theta ]
then\; use\; H_{f}\geq H_{i} \;[ for\; stable\; equilibrium]
then \; u\;get\;R\geq a
(equillibrium*)
