1is this right nishant sir?????
the right block is fixed. the left block has velocity v=√2m/s at any instant AB=R√2 right block has friction.
all other surfaces are frictionless what is the velocity of center of mass of cylinder at this instant
give answer in terms of mass if needed as i don't remember exactly
-
UP 0 DOWN 0 0 8
8 Answers
1AB was R√2 as far as i remember...
so, that means angle AOB (where O is the centre) = 90o
the sphere will rotate about A...so, instantaneous vel of O is along OB
also, for surfaces to remain in contact, component of velocity along common normal of both the points (one on the sphere and one on the block) should be same.
so, component of v along OB = vel of O
=> vel of O = √2cos(45) = 1m/s
1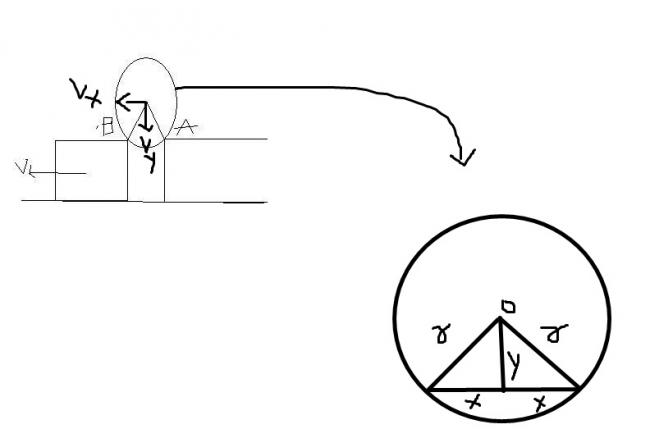
x^2 + y^2 = r^2
differentiating both sides with respect to t
2x (dx/dt) + 2y(dy/dt) = 0
dx/dt = Vx
dy/dt=Vy
xVx=-yVy
Vx=√2/2=1/√2
so Vy = -(x/y)Vx
as x=r/√2
and x^2 + y^2 = r^2
so y^2=(r^2) - (r/√2)^2
y=r/√2
so Vx=Vy
and
Vcom=√(Vx2 + Vy2)
so
Vcom=√(1/2)+(1/2)=√1=1
1but dx/dt will give us the velocity in x direction for any point on the circumference of the circle na not of center........
1i'm afraid arshad's ans is wrong...we did this question in class today...and sir did it in the same way as i had posted in #2.
but i dunno why arshad isnt getting the ans...method seems correct to me..
3Arshad the eqn of the circle does not have a fixed center,bcos the circle has translational motion too,but u have differentiated the circle eqn which means dat u havent taken the translational effect.