1Yes Subho rocks....
and virang you can go upto cos 89.999999999999999999.... degrees in taking the cos component of N but please no 90 degrees as it's now perp. to the N-vector. :-)
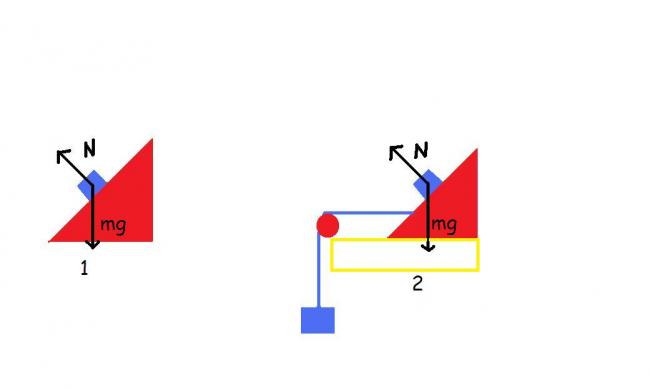
See when we taken into consideration banking in circular motion. We resolve the normal force along the x and y axis. We get Ncosθ = mg
θ is the angle of banking.
When we consider inclined plane we get N = mgcosθ. See both N are the same but the value is different.
-
UP 0 DOWN 0 0 22
22 Answers
49noooooooooooooo...i had the same dbt once...
then i got it solved thus.... i l post in a momment now...
111Therefore in case of the car in banking the car is accelerating towards the centre therefore we apply case 2. Am i rite?if i am then i understood it.
49in case 2,
the block tries to remain in its own position...i.e net accn in downward direction is taken to be zero so we take, Ncosθ=mg...[1][1][1]
49now in the above two cases,
suppose the system is completely frictionless...
in case 1,
the block accelerates down, so the entire force in downward direction is not being balanced...but there in no accn in direction perpendicular to the inclined plane...so net forces in that direction sums up to zero...thus, mgcosθ=N
49ohh sorry i forgot to post solution.......
[2][2][2]
aaj kal bara bhulakkar ban gaya hoon!!
[2][2][2]
6hey is wat i said is correct??even to some extent??
1and even if you do take it.....the slant will become a horizontal plane !!!!
There will be need of banking then !!
1virang......how can you ever take a vector component in a perpendicular direction ??????
NO VECTER HAS A COMPONENT IN ITS PERP. DIR ... !!!!!!!!!
AS COS 90 is always EQUAL TO 0 !!!!!!!!!!!!
11ok
It is a good doubt
Sorry for such a title
See my argument is
when you we broke N into its component we get
N cosθ = mg
Therefore when θ = ∩/2
Then N becomes infinity . thats wrong rite. See when θ = ∩/2 the contact force becomes zero and the body under goes free fall. Therefore i think it is wrong to resolve N into its component.
So...the doubt comes back?
One more thing is that when we considered Ncosθ =mg We considered no acceleration in the y-axis but the body could slide down the slope .
What do you think now?
1And please don't call doubts stupid...that may be easy but still a doubt.......I really feel ashamed when you say this.............................................cause I myself have millions of doubts.. :-)
1I can see no error in it .
In the prvs case youhad broken mg into its components.......now you've broken N into components.
It's simply for your convenience the method you choose.
Both of them are bound to give the same result......at least I'm getting so.
11See my doubt is can we consider banking a inclined plane ? . If so in inclined plane N =mgcosθ
But while proving tan θ = v2/rg
We consider Ncosθ= mg. Both the N are same but the value is different.
How is this possible?
1Yes Anant Sir is right.
N = mg cosθ as there's no acceleration in Y-direction.
Here Y is not the vertical axis....it is the perpendicular to the slanting ground.
66N ≠mg cosθ since there is an acceleration down the incline. But there is no acceleration in the vertically up direction (the acceleration is towards the center of the circle which lies on a horizontal plane passing through the object). Hence N = mg cosθ.
6you have to resolve forces along the radius in circular motion....same in banking....coz the motion takes place along the radius...