9
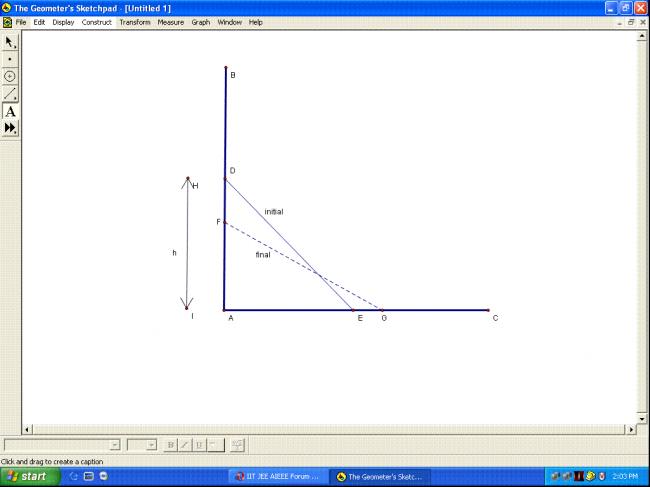a rod is aligned at a corner as in figure. no friction is there anywhere. it start to slide. prove that it would leave the vertical wall when it's tip is at a height 1/3rd of initial.
edit:: the actual question asked 1/3rd height fallen or "leave the vertical wall when it's tip is at a height 2/3rd of initial". my question was wrong previously...
-
UP 0 DOWN 0 3 35
35 Answers
9sorry
i used torque a Nl/2 but it should be multiplied by sinθ
aneway that wont affect result as in rhs i used α instead αsinθ
62I think it is irodov.. or resnick halliday..
irodov in most probability
*edit.. not irodov.. just checked!
May be a JEE question! but again a very common question... pity i dont remember the source!
1acclereration of the end point will not be ay/2 it will be 2ay
and how are you getting
W-N=may/2 (shoudnt it be "may")
and how αl=ay?
9i kept ay as acc of endpoint downwards
then ay/2 will be its acc wrt com
also ay/2 is abs acc wrt our frame
hence w-n=may/2
9and yes i observed centre of mass is moving along a circle
but how do i proceed
1so as the com moves in a circle , its direction of velocity at any instant =tangent to the circle!!
so just move it from θ1 to θ2 and conserve energy (as normal rection doent "work" here)
then its up to you!!
1
wrting the soln for a general θ1 will be tedious (i feel lazy)
let the length of the rod be 2L
ok so let me write the full solution for he case when θ1=90 (i.e when the centre of mass is at a height L)
and let θ be the angle at which the rod loses contact from the wall
as it loses contact from the wall we can say that at that point of time the acceleration of the centre of mass of the rod towards the horizontal direction is zero (as there are no forces in that directions)
first the work done by normal reactions on both the sides is zero( as the point of application of normal reaction moves perpendicular to the normal reaction)
so we can conserve energy
intially kinetic energy = 0 and potential energy = mgL
finally potential energy =mgLsinθ
and let final kinetic energy = (1/2)mv2
then by conservation of energy
mgL=mgLsinθ+1/2mv2
we get v2=2gL(1-sinθ)
but as in the final state the rod loses contact with the wall ax=0
and further we observe that the centre of mass is moving in a circular path
hence the velocity of the centre of mass at any instant will be at the tangent to the path
so in the final state the velocity of the centre of mass makes an angle of 90-θ with the horizontal
so acceleration in that direction =
d(vsinθ)/dt=(d(vsinθ)/dθ)*dθ/dt
as the above quantity is zero in the final state
we get (d(vsinθ)/dθ)=0 or dθ/dt=0 --- (i)
but dθ/dt cannot be zero (af the centre of mass has velocity = Ldθ/dt as it is moving in a circle)
so d(vsinθ)/dθ=0
but v2=2gL(1-sinθ)
so v2sin2θ=2gLsin2θ(1-sinθ)
diffrerentiating both sides w.r.t θ
2vsinθd(vsinθ)/dθ=4gLsinθcosθ-6gLsin2θcosθ
from (i)
0=4gLsinθcosθ-6gLsin2θcosθ
we get sinθ = 2/3
that means it will leave the wall when sinθ=2/3
hence height of centre of mass at that instant = Lsinθ=2L/3
height of tip=2*(2L/3)=4L/3
intially the height of the tip was = 2L
so the tip now leaves the wall when its height is 2/3 of the original height
(just realized now , in the question it should have been 2/3rd)
1oh! i apologize. its 2/3rd. anyway i had calculated it would fall 1/3rd by thge time :)).
1in general if the rod started sliding from vertical position:::
step1.. IAOR : (l cos θ, l sinθ).
step2. mgl/2 (1-sinθ)= 1/2 Iw2 , I= 1/3 ml2
step3. 2w dw/dt = -3g/l cos θ dθ/dt so, α=-3g/2l cosθ.
step4. C.M.=(l/2 cos θ, l/2 sinθ) ax= - w2l/2cosθ - αl/2 sinθ.
step5. we require Fx=0 i.e. ax=0.
step6. put val. of w and α, sinθ=2/3.
if initial height=h, folloe same process to get the answer sinθ=2/3 sinλ where λ= initial angle with horizontal.
9if its 2/3 rd then my previous solution is perfectly right
9not my first post i realised my mistake of considering it as pure rotational
see my second post i got 2/3h easily
1u have not considered the normal reaction from the other wall
and torque for N will not be Nl/2
62Yeah even i was wondering this is a standard but good question!! A beautiful one. If you know the "real" logic behind this one.. you know a lot of stuff :)
Probably enuf for IIT JEE!
1actually i had solved it by the centre of mass method wheres ithpower had done it using rotational mechanics
9normal reaction from other wall is 0 as it leaves the vertical wall
yes ive used torque as Nl/2 only