hello!!! anyone plz help me out with this problem.
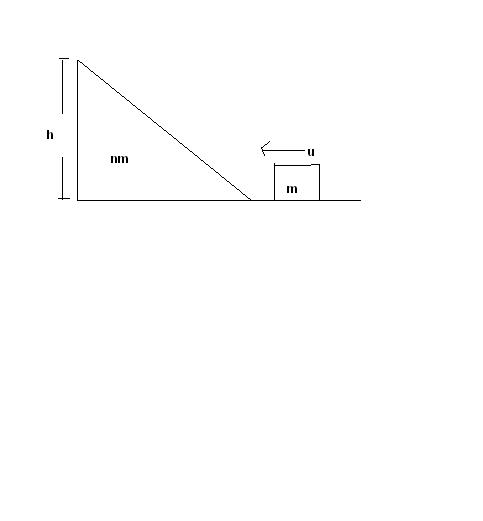 .
.
A block of mass m is pushed towards a movable wedge of mass nm and height h with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is...
a> √2gh
b> n√2gh
c> √2gh(1+1/n)
d> √2gh(1-1/n)
-
UP 0 DOWN 0 0 10

10 Answers
The question's done but first assure if the wedge is fixed or not..........bye for now...rath's tuition ...no time to post soln.......i can post it tonight.
First use conservation of linear momentum...
During this period mu=(M+m)V
you get the final v in terms of u (v here is in the horizontal direction)
Now conserve energy.. to take mgh+ 1/2 (m+M) (v2) = 1/2 m u2
Can you solve now?
I think my procedure is correct.But ask Nishant bhaiya to check my ans.....
here is the ans..:
let v is the final velocity of the system..
mu =( m+nm) v
v= u/(1+n).
1/2 u2= 1/2 (1+n) v2+ gh
now put the value v=u/(1+n)
then,
u2=(1+1n)2gh.
hence opt C is correct..
then please post it here so that the thread can be closed swastika [1]
Considering nm=M
mu=(m+M)v
therefore, v=mu/M+m.................(1)
1/2(m+M)v2 +mgh=1/2(mu2).............(2)
putting (1) in(2)
1/2mu2-1/2{(mu)2}/(M+m) = mgh
Solving it...by replacing M=nm.
u2(1-[m/(nm+m)])=2gh
furthur solving it.
I am getting opt c is correct.