pls WORK OUT these sums for me
1)If a1 and a2 are two non-collinear unit vectors and if (Modulus)[a1+a2]=√3 ,then the value of (a1-a2).(2a1+a2)is
(a)2 (b)3/2 (c)1/2 (d)1
2)A particle moves on a given line with a constant speed v.At a certain time it is at a point P on its straight line path.O is fixed point.The value of (OP X v)is :(where y is perpendicular distance from O to given line)
(a)-yvk^ (b)-2yvk^ (c)-3yvk^ (d)none
3)A plane is inclined at an angle of 30° with the horizontal.The magnitude of component of a vector A=-10k^ perpendicular to this plane is(here z-direction is vertically upwards)
(a)5√2 (b)5√3 (c)5 (d)2.5
4) Integrate w.r.t x : (2x+9)5
-
UP 0 DOWN 0 0 4

4 Answers
answer no. 4......... let 2x+5=t
dt/dx=2
dt=2dx
multiply the numerator and denominator of the expression by 2
in numerator : 2dx=dt & (2x+5)5 = t5
now integrate t5 dt and multiply by 1/2.........
1)
|a1+a2|=√3
|a1+a2|2=3
(a1+a2).(a1+a2)=3
a1.a1+a2.a2+ 2a1.a2
|a1|2+|a2|2+2a1.a2=3
1+1+2a1.a2=3 (unit vectors)
a1.a2=1/2
(a1-a2).(2a1+a2)=2a1.a1+a1.a2-2a1.a2-a2.a2
=2|a1|2-|a2|2-a1.a2
=2-1-1/2=1/2

Considering the plane to be xy, outward normal to the plane as +z direction and motion of particle in clockwise sense (these were not mentioned in the question)
let the angle between OP and PR be θ
(OP)X(PR)=|OP||PR|sinθ n^=|PR|(|OP|sinθ) n^ =|PR|.|OQ| n^
=vy n^= -vy k^ (from right hand rule)
Alternately (1/2)|aXb| gives the area of the triangle formed a and b
so area of triangle is (1/2)*v*y=vy/2
|OPXv|=2*area=vy
direction for right hand rule is -k^
so it is -vy k^
3)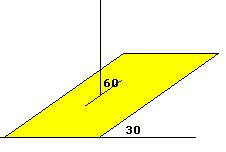
angle between the vector and plane is 60°
so the angle between the normal of plane and vector is 30°
magnitude of component of vector A along normal =10cos30=5√3