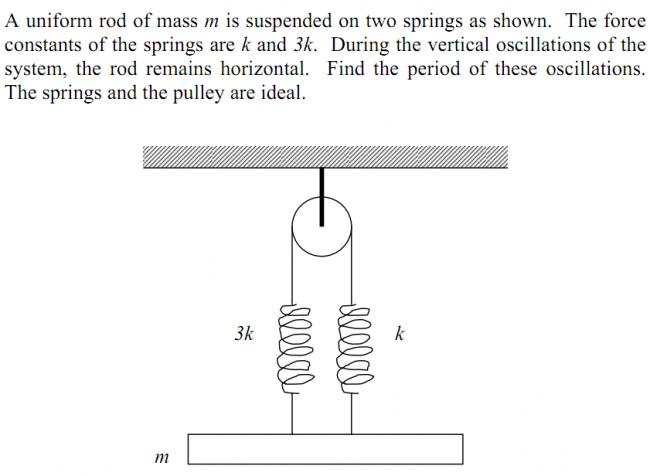
1let the extension in the right arm be x1 and in the left arm be x2
since the Tension is same every where in the string(as it is massless) we have
3kx_1=kx_2\\ 3x_1=x_2\\ \\ \text{now the total extension is equally shared in both arms,so...} \\ \\ \frac{x_1+x_2}{2}=2x_1\\ \text{this would have produced the same effect if there were a spring of spring constant }\\2k \because\boxed{ 3kx_1+x_1=mg \ \Leftrightarrow \left ( 2k \right )\left ( 2x_1 \right )=mg}\\ \text{So the time period of oscillation is }\boxed{T=2\pi\sqrt{\frac{m}{2k}}}}
P.S --> sorry to answer it as it was addressed to nishant sir or kaymant sir , so the chances of the solution being wrong is high :P
1thanks for the try.But the answer you get is not correct.This problem is difficult due to the presence of pulley.If the pulley is not present the problem becomes very easy.There are many problems in H.C. Verma without pulley.Can you have a source to call KAYAMAT or NISHANT sir??If yes please please call them to discuss this problem.Thanks in advance.
21let the displacement of m in vertical direction be x
so the total elongation in both the springs will be 2x
let the elongation in 3k spring be p and in the other one be q (p+q= 2x.....1)
now if the mass m has to stay horizontal the string must slip over the pulley ( i took a lot time to realize the fact)
equating torques 3kp = kq
or 3p= q.....2
so net force = mg+ 3kx (solving 1,2)
so a=-(3k/m) x
so T=2∩√m/3k
21a small edit: in post #10 net force means net force given by springs...
21@ amrit
as the two springs are symmetrically connected after equating torques
we get 3kp= kq
cancelling k from both sides i wrote 3p=k (As k≠0 :P :P )
1@ Shubhodip
actually i am talking about the step a=-(3k/m) x
Actually you write this step directly,but it not a direct step.There is lot of hard work to get this tep.I know ho to get it.But it just want to know how you get this step?can you please tell me how you get this step?
