If two circle touch each other, at their highest or lowest points, and a straight line be drawn through that point to meet both circles, show that the time of sliding down form rest down the portion of this line intercepted between the two circle is constant.
-
UP 0 DOWN 0 0 1

1 Answers
Consider the following diagram.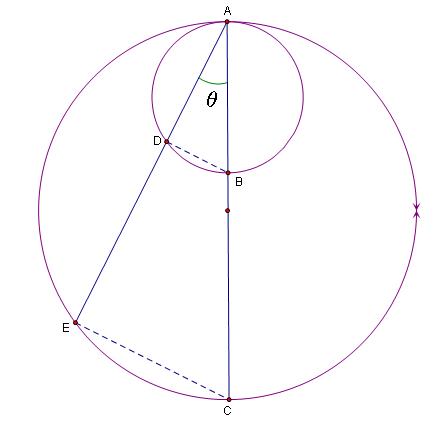
Let the radius of the bigger circle be R while that of the smaller circle be r. Its easily seen that ADB is a right triangle and so is AEC. Hence, we get
AD = 2r cos θ and AE = 2R cos θ.
So that
DE = AE - AD = 2(R-r) cos θ
On the other hand the acceleration along the segment DE is g cosθ. So the time taken is obtained by
12 (g cosθ) t2 = DE = 2(R-r)cosθ
from where we obtain the time
t = 2√(R-r)/g
which is independent of θ and accordingly constant for a given pair of circles.