anyone????????????????
A loop of rope is whirled at a height with angular velocity omega,so that it becomes taut in a circle of radius R.A kink develops in whirling rope.Find the speed of kink in the rope.
Under what conditions does the kink remain stationary relative to observer on the ground?
Linear mass density of rope is "mu".
-
UP 0 DOWN 0 0 8

8 Answers
i think it is a disturbance,,,,,,,,,sort of pulse............u can see it at the top in my figure...............
Its not so scary as it looks like.
We know that velocity of a wave in a string =√T/μ
where T is the tension in the string.
In order to calculate tension, take a small element dθ at angle θ
Considering force balance in the radial direction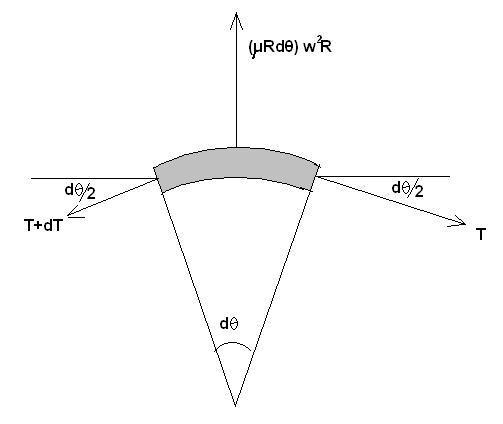
(T+dT) sin dθ/2 +Tsin dθ/2 =(μRdθ)ω2R
for small angle dθ/2
sin dθ/2≈ dθ/2
and dT*dθ/2 ≈0
hence, we get Tdθ=(μRdθ)ω2R
or
T=μR2ω2
therefore, velocity of kink=√T/μ
=Rω
Hence, with respect to the observer on ground, the kink will remain stationary when the motion of kink and ω are in the opposite direction and will move with 2Rω if they are in the same direction.