ans is 0.30 m
6 Answers
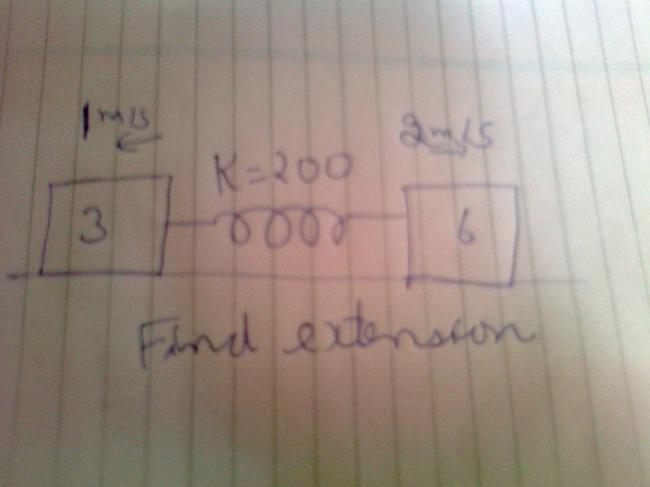
assumption : spring is initially relaxed
vc=1 m/s
v3/c =2 m/s
v6/c=1 m/s
in the com frame ,
extension is max when vel of 3 and 6 become zero.
the KE lost in dis frame is stored as PE of spring
so 1/2 (3)(2)2+1/2 (6)(1)2=1/2k(x)2
9/100 = x2
x=0.3 m
u can see it as
Energy of the system = KE of system wrt COM + KE of COM + PE of spring
now KE of com = constant since no external force is acting
and energy of system = constant
so KE of system lost in COM frmae will come as PE of spring
so PE of spring = max when all KE in COM frame is lost
you can solve it another way also
let 6 kg mass = m1 , 3 kg mass = m2
as the spring is streched the kinetic energy of masses is being converted into spring's potential energy ....the extension wud be max when both the masses will move with same speed
by conservation of energy
kinetic energy of blocks initially = kinetic energy of blocks (when both move with same speed)
+ potential energy of spring (at that time) --(1)
by conservation of momentum
m1v1 - m2v2 = (m1 + m2)v
(v = thier common velocity finally)
you will get v = 1 m/s
from (1),
total KEinitial - total KEfinal = 12kx2 - - - (2)
total KEinitial = 12m1v12 + 12m2v22 = 27/2
similarly total KEfinal = 12(m1 + m2)v2 = 9/2
applying these values in (2) and solving for x
we get,
x = 0.3 m