1plz help me with these questions friends!
1
varun.tinkle
·2010-12-23 03:54:02
1st one is a direct application of a simple concept .... a=gsin@/1+I/mr^2
thereofre the sphere with the least I will come 1st therefore a disc
1
varun.tinkle
·2010-12-23 04:02:01
2) let us seek to mathmatically derive in an acc frame
suppouse L=mvrsin@
now dl.dt = mrsin2 a here a depends upoun that frame so if wveryhting is measured from non inerial frame dl/dt= torque holds
abt L=iw i think here there might be some changes coz with different reference frames the axis of rotation changes from 1 frame there a motion is only translatory but from other purely rotational therefore i will go for b
1
varun.tinkle
·2010-12-23 04:10:00
3) this is a gud some the prob is that it is a non rigid body
now for simple treatement let us consider two masses having a vel v1 and v2 and mass m1 and mass m2 so it can be approximated as a non rigid body for calculations
now one things for sure moment of inertia will not remain constant say v1 and v2 are in opp direction so they will contune and moment of inertia will not remain constant
same with k.e. now form work energy theorem the work done by all ext and interntal forces is change in k.e. so
now in linear momentum will remain constant
coz form newtons 3rd law they exert equal and opp forces on each other.....
now abt angualr momentum
well this thing i am not exactly sure.... coz in a rigid body i am dea sure the sum of internal torques=0 so i am 90% sure that torques will be non zero in a non rgid body
now
dL/dt=torque therefore angular momentum will not remain constant....
1
varun.tinkle
·2010-12-23 04:14:03
4) this is a cakewalk
now conserving linear momentum
mv=Mv1
v1=mv/M
now ocnserving angular moentum abt the mid point of the rod
mvl/2=Ml^12w
now w=6mv/Ml
now vel of the end 3mv/M now total vel
=4mv/M
if M=4m then its an elastic collision
1
rajat.sethi rajat
·2010-12-23 07:39:00
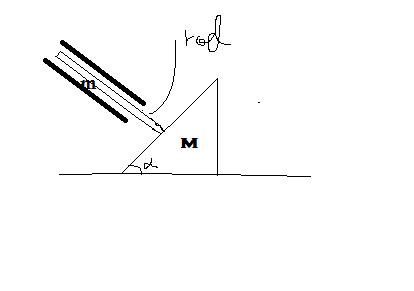
The rod of mass m is held by 2 smooth walls always perpendicular to the surface of the wedge of mass M.give the relationship b/w the accelarations of the two.All surfaces are smooth.
am=aMsin(alpha)
11Hint : - For the rod and wedge to remain in contact , the component of acceleration perpendicular to the contact surface must be same.