what is its eqn of motion??
i am confused abt the trajectory of the block..... wht path will it follow.....
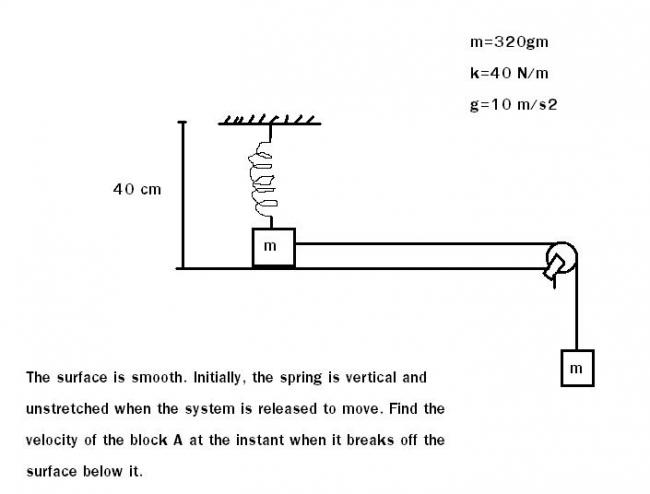
the block attached with the spring is block A
-
UP 0 DOWN 0 1 17

17 Answers
Trajectory will depend on the relative masses of A and B
If B is very heavy, the block A will fall verticallly down after breaking off the surface.
If B is slightly greater , it will offcourse follow a parabolic path.
If I do everything what shall you do? lol
equate the forces on the block A when it breaks off the surface....find its resultant acceleration.
Now use equations of motion with x-component and y-component of acceleration.
EDIT: I mistook block A and B
If A is very heavy, the block A will fall verticallly down after breaking off the surface.
If A weighs slightly less (B is more), path of A will be parabolic because initially, its acceleration is along the surface, after breaking off the surface, acceleration due to g acts upon it which is vertically down. Resultant acceleration is south-east. So it will follow a parabolic path.
You might ask what is the difference if A is very heavy.
Its acceleration along the surface would be very very less compared to g
So there won't be any significant horizontal motion after breaking off the surface.
It falls vertically down.
The path of the block A will be along the surface because its acceleration is along the surface.
I meant that the spring breaks from its point of contact with the block A.
If you say that the spring never loses contact, then the block will never fall down.
Just after the spring loses contact with the block, the restoring force will vanish and when the block breaks off the surface, normal reaction by the surface will be 0.
from conservation of energy it can be done...
the equation is
2(mv2/2) [k.e of the two block at that instant] - mgh(h is the distance moved from t=0)
+ Kx2/2 [x is the elongation of spring] = 0
now L(length of unstreached spring ) ,h and L+x forms a triangle..let the angle between L+x and h be ∂, so Kxsin∂= mg (at the instant of breaking)...
so Lcosec∂ - L =x
after eliminating h and ∂ and x we get the velocity....
however, i'm not 2 clear abt d trajectory of the block after it leaves contact with d surface.
please TRY, SOME1!
m= 320g = 0.32kg
k = 40N/m
h = 40cm = 0.4m
g = 10 m/s2
From the free body diagram,
kx cos (theta) = mg
(when the block breaks off R = 0)
cos (theta) = mg/kx
So,
0.4/(0.4+x)=3.2/(40x)
or, x=0.1 m
or, s=AB=√(h+x)2-h2=√0.52-0.42=0.3
Let the velocity of the body at B be v
Charge in K.E. = work done (for the system)
(1/2 mv2 + ½ mv2) = –1/2 kx2 + mgs
or, (0.32) × v2 = –(1/2) × 40 × (0.1)2 + 0.32 × 10 × (0.3)
v = 1.5 m/s.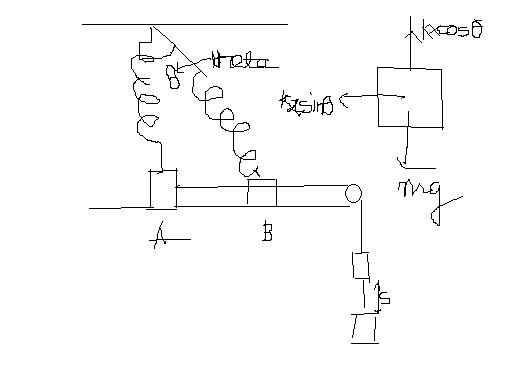
please strain ur eyes 2 decipher my figure:)
@ swordfish: the spring doesnt break. the block loses contact with the surface. so, restoring force is never 0.
Make a FBD of the block A.
At the instant the spring breaks, tension in the spring (restoring force) will become 0.
hw shud i proceed to solve....
shud i take the resultant forces acting on the block.....