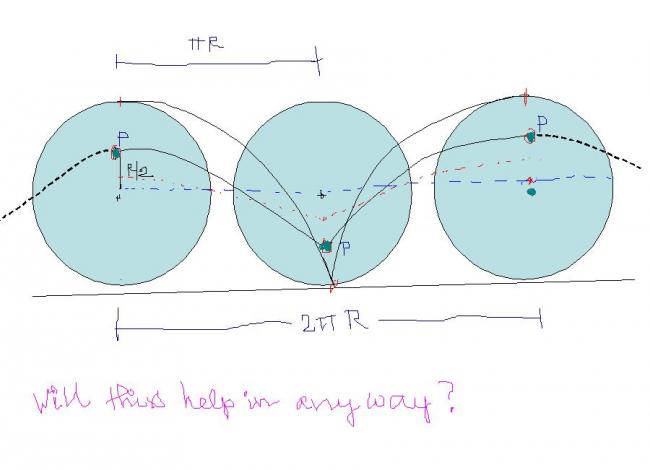
U have to find radius of curvature..
A sphere is rolling on the rough surface without any slipping at the contact point. Find the radius of curvature of the trajectory of the point which is at R/2 just above the center...
i don't know why i messed this [2]
-
UP 0 DOWN 0 2 11

11 Answers
i think you have to write the eqn of the cycloid in which that point moves
did you try that ?
top most point moves in a semicircle of radius Î R.
centre ................................................... ∞ .
then wat can be the relation in the in-between points .. ??
can neone figure out ??
since the point moves on a cycloid,
the radius of trajectory will keep on changing;
it will depend on the position of point.
polar equation of a normal cycloid is:
x=a(θ+ sinθ);y=a1(1+cosθ);
here a=R;a1=R/2;
radius of curvature=((1+y12)3/2)/y2
where y1,y2 are ist and 2nd derivatives....at that point.....
The velocity of the point :
\frac{3}{2}\omega R\Rightarrow a_n=\omega ^2R/2
\Rightarrow \rho =\frac{\frac{9}{4}\omega ^2R^2}{\omega ^2\frac{R}{2}}=\frac{9}{2}R
why butt in such cumbersome calculus ?