but sir why 2x is the elongation .... please explain sir [2]
The disk has a weight of 100N and rolls without slipping on the horizontal surface as it oscillates abt its equilibrium position . If the disk is displaced , by rolling it counterclockwise 0.4 rad, determine the equation which describes its oscillatory motion when it is released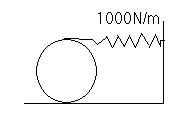
θ = 0.4 cos16.16t
-
UP 0 DOWN 0 0 5

5 Answers
During the motion let at any instant the center of mass is displaced by an amount x to the left from the equilibrium. At this instant the elongation of the spring is 2x. The total energy of the system is a constant:
\dfrac{1}{2}mv^2 + \dfrac{1}{2}\cdot \dfrac{1}{2}mR^2\omega^2+\dfrac{1}{2}k(2x)^2=\text{ constant}
The first two terms represent the total kinetic energy, v being the center of mass velocity.
Since there is pure rolling, therefore v=Rω. The above equation therefore becomes
\dfrac{1}{2}\cdot \dfrac{3}{2}mv^2+\dfrac{1}{2}k(2x)^2=\text{ constant}
Differentiating w.r.t. time t, we get
\dfrac{3}{2}mv\dfrac{\mathrm d v}{\mathrm dt}+4kx\dfrac{\mathrm dx}{\mathrm dt}=0
Since dx/dt = v, we get ultimately
\dfrac{3}{2}m\dfrac{\mathrm d^2 x}{\mathrm dt^2}+4kx=0
where I used the fact that d2x/dt2 is same as dv/dt. Rearranging the terms we get finally
\dfrac{\mathrm d^2 x}{\mathrm dt^2}+\dfrac{8k}{3m}\,x=0\quad \Rightarrow\ \dfrac{\mathrm d^2x}{\mathrm dt^2}+\omega^2x=0
(Note that this omega is not the same as the angular speed for which I used the same symbol unfortunately)
As the center of mass performs an SHM with angular frequency \omega =\sqrt{\dfrac{8k}{3m}}
And hence the motion is
x=A\cos(\omega t+\varphi)
In this case we are looking for the angular motion, which would be due to the relation Rθ =x, becomes
\theta =\theta_0\cos\omega t
where θ0 = 0.4 rad.
When a circular body is rolling, how are the velocities of the center and the highest point related?
velocity at the centre = V
velocity at topmost point = V + Rω = 2V
velocity at the bottom most point in contact with the ground = V-Rω = 0
oops sorry had forgot abt that , and didn't mark the question rightly as it was given that the body was rotated anticlockise to give an elongation .
SRY sir just had forgot abt that .
THNK U SIR ans Govind for clearing me......[1]