Mechanicssssss!!!!

Ok.

The question is not so Difficult as it seems. Nevertheless from the question itself it is clear that the particle follows the circular trajectory only upto certain height and then the string attached to it becomes slack as it begins a parabolic trajectory.

How to Solve: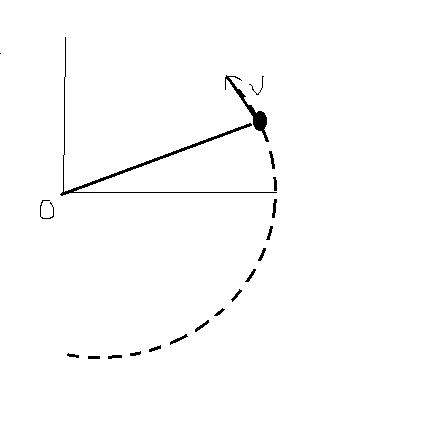

Let at this instant the angle made by the string with the horizontal be θ. It is the instant when the circular motion of the particle ceases. The velocity vector at this instant is shown in direction and at angle θ with the vertical.

Using Conservation equations and Circular motion equation we can find out the velocity of particle at this position.

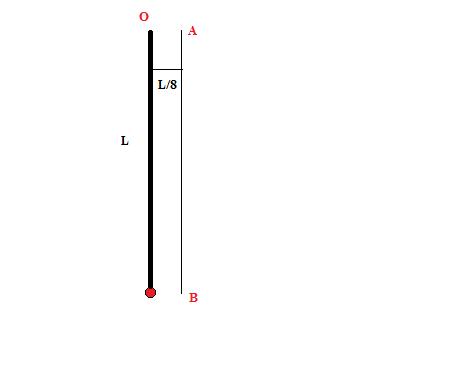
Now the vertical line AB is at a Distance L/8 from O, So for the projectile motion of the particle it should be such that it is at it's highest point of motion (So that it has only a horizontal velocity) when it crosses the line AB.

From these we can easily solve.

Just building up on what vivek said

if T be the tension, u be vel at lowest point, we have the eqns
T + mg cos @ = mv^2 /r
Conservation of energy equation
and ( l sin@ -l /8) / v cos@ = v sin @ / g

note @ is the angle made by string from the vertical

also use the fact when the particle breaks away, T = 0

I think the confusion lies in the fact that what if the particle breaks away before the line AB. I must admit i dont know anyway to disprove this.