iz the ans
mv^2/2Ï€ r
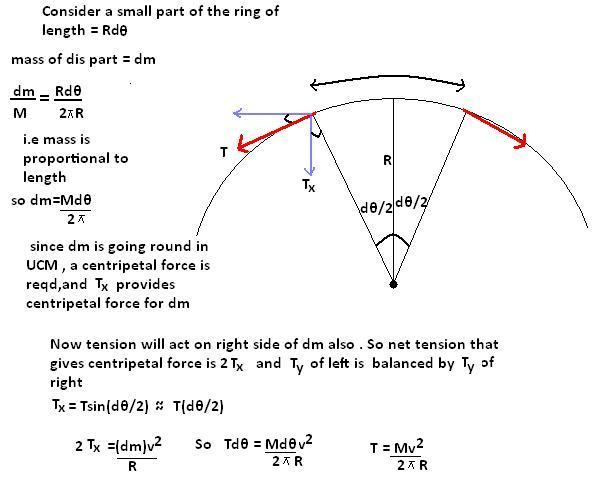
A metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
-
UP 0 DOWN 0 0 10

10 Answers
this ques was asked by me nd answered by qwerty bhaiyaa already itss a HCV ques (example).............
http://targetiit.com/iit-jee-forum/posts/circular-motion-easy-doubtsss-13650.html
i tell u the simplest way of finding tension
first of all calculate total force acting on all elements (scalar sum of all forces acting on particle , BUT NOT VECTOR SUM)
i.e \int \left|dF(x) \right|
i.e in this question it is \frac{mv^2}{r}
divide this by 2\Pi
by doing this u easily get answer
try this method (it is correct in 99.99% cases)
example:
let a non conducting metal ring which has +Q charge (uniformly distributed on ring) & a another -Q charge is placed at ring's center
find tension in ring (radius= R)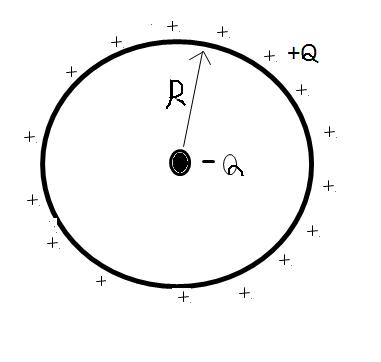
solution:
TOTAL FORCE acting on ring is -\frac{kQ^2}{R^2}
divide it by 2\Pi
so tension in ring is \frac{kQ^2}{2\Pi R^2}
(sorry,assume +ve charge on center element in case of finding tension ...if -ve charge is assumed then there will be no tension but compressive stress )
Harsh , is ur trick applicable only for circular rings or even other geometrical bodies?
i only applied on rings (where uniform distribution)
in other cases divide force by solid angle
i.e in case of sphere divide by 4\Pi
( NOTE : uniform distribution is required i.e charge,mass etc. )
(uniform distribution provides equal magnitude of force on unit elements)
in straight rode there is not equal force on unit elements
I REQUEST U TO APPLY THIS ONLY ON RINGS...[9][4]
I REQUEST U TO APPLY THIS ONLY ON RINGS...[9][4]
I REQUEST U TO APPLY THIS ONLY ON RINGS...[9][4]
I REQUEST U TO APPLY THIS ONLY ON RINGS...[9][4]
I REQUEST U TO APPLY THIS ONLY ON RINGS...[9][4]
I REQUEST U TO APPLY THIS ONLY ON RINGS...[9][4]