24tell me how did u get those 2 eqns????????????
A spring mass system is held at rest with the spring relaxed at height H above the ground.Determine min. value of H so that given system has tendency to rebound after hitting the ground.
Given coeff of restitutuion between m2 and ground is zero.
-
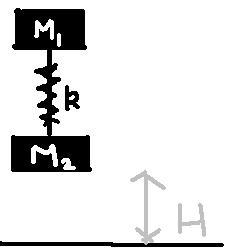
UP 0 DOWN 0 1 5
5 Answers
1(kx)2=2m1g(kx+m2g)+(m2g)2
kx2=2m1gH
just solve for H
u will get the ans
1I can tell you the thing ,
the condition that the lower block rebounces is
x > M2g/k because just draw the free body diags , statics problems thats the key
1/2 M1 v^2 = 1/2 kx^2 + M1 gx
also , kx = M2g
So ,
2M1 gh = k(M2g/k)^2 + 2M1g(M2 g/k) this should give the answer !
Please tell me if they are correct !! Been so out of touch :(
62
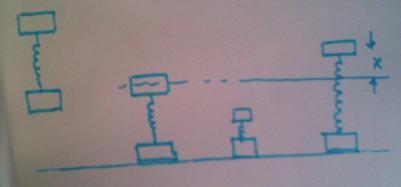
Here x will be such that kx=m2g
so x= m2g/k
Energy just after colission (state 2 in the figure) (The KE of the lower mass gets lost!)
= M1gH
Energy just at extension x will be M1gx+1/2kx2
We know x..
So we know H!
btw i think i am getting the same answer as Diptosh :)