i dont have the ans .someone pls verify the ans
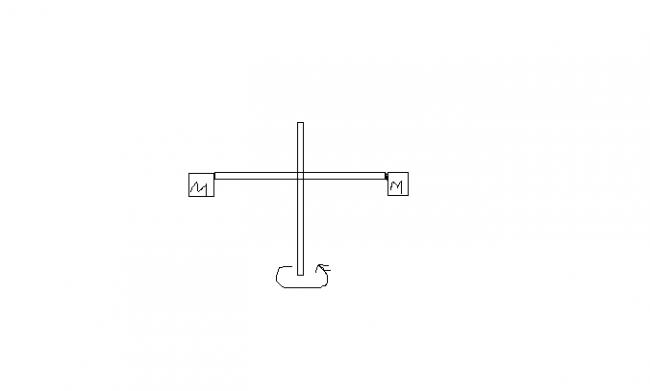
two blocks each of mass M are connected to the ends of a light frame as shown in figure. the frame is rotated about the vertical line of symmetry the length of each side being l.the rod breaks if the tension in it exceeds t. find the maximum velocity with which the frame may be rotated without breaking the rod
hcv soln. t=Mv2/l
what will be the velocity if masses are M1 & M2
-
UP 0 DOWN 0 1 4

4 Answers
the centripetal force require for circular motion is mv2/r
so this centripetal force is provided by tension force
mv2/r=t v=√tl/m
if masses are m1 and m2 then centre of mass from axis of rotation is x=(M1L - M2L)/M1 + M2 .
t=(M1 + M2)v2/x
v=√xt/(M1 + M2)
lalit i dont know why but theres no flaw in ur answer
but lets try to solve the sum withouth cm concept
then T=m1w^2r
and T2=mw^2r
so we r getting t1 and t2 as differnet since it is a rod
pls correct me if i am wrong there can be differnet tensions so in each part we hv to check that whether t is greater than t0
it sounds absurd........ doesnt it
anyways i am trying to find a flaw in either my argument or lalits but cant so pls help out
Consider one block having angular velocity W.
Then V= L W.
Acceleration towards the centre is V2L.
Multiply this by mass of the block, and you get centripetal force.
The rod breaks if this force exceeds tension.
Hence,
T = M V2L
So, V = √(L TM) is the maximum velocity it can be rotated.
W = VL = √(TM L) is the maximum angular velocity it can be rotated at.