ncert mod qn-3.28

3.28 The velocity-time graph of a particle in one-dimensional motion is shown in
Fig. 3.29 :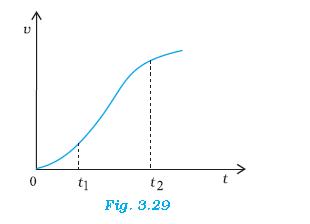

Which of the following formulae are correct for describing the motion of the particle
over the time-interval t₁to t₂:

(a) x(t₂ ) = x(t₁) + v (t₁) (t₂ – t₁) +(½) a (t2 – t1)²
(b) v(t₂ ) = v(t₁) + a (t₂ – t₁)
(c) v_average = (x(t₂) – x(t₁))/(t₂ – t₁)

(d) a_average = (v(t₂) – v(t₁))/(t₂ – t₁)

(e) x(t₂ ) = x(t₁) + v_average (t₂ – t₁) + (½) a_average (t₂ – t₁)²

(f) x(t₂ ) – x(t₁) = area under the v-t curve bounded by the t-axis and the dotted line
shown.

pls explain why the options a,b and e are ruled out.