the answer is 2r0ω2eωt
since the part tests must be coming now..i guess the first part test must be having mechanics in it
this question had come in my fiitjee aits (or might be some phase test)
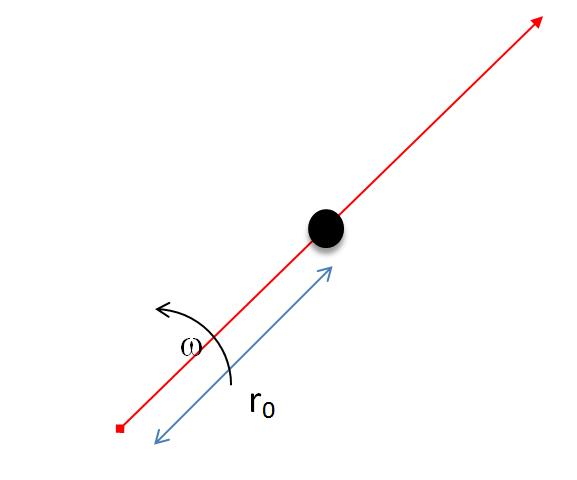
there is a smooth rod(friction is absent on its surface),a bead of mass m is inserted in it and is at a distance of r0 from the centre of rod ,the rod is now rotated about the centre with a constant angular velocity omega..the length of rod extends to infinity…
find the normal force experienced by the rod as a function of time…
-
UP 0 DOWN 0 0 4

4 Answers
ω2r = vrdvdr
integrate both sides ( vr = radial vel )
(ωr)2 = vradial 2
vradial = rw =drdt
again integrate
[lnr] = [wt] , t=0 , r = ro
so r = roeωt
at any r , torque of normal abt hinge, = rate of change of ang momentum abt that hinge
Nr = dLdt = ddt (mr2ω ) = 2mrω (vr )
so N = 2mω(vr ) = 2mω (rω) = 2mω2roeωt
so net normal = √ (2mω2roeωt )2+(mg)2