does this have anything to do with calculus?
a bomb bursts at t=0 and the small pieces fly off in every direction....
a man is standing at a distance of 30 m frm the place where this bomb blast occurs
if the velocity of all the pieces vary upto 30 m/s (max vel. is 30 m/s)
then prove that the man is in danger for 5 s....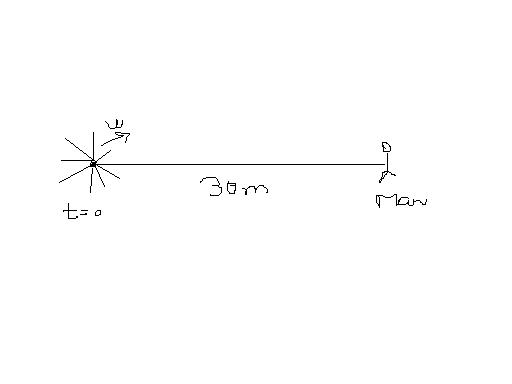
-
UP 0 DOWN 0 0 5

5 Answers
Hint:
Find the envelop of the flying particles which were launched with the maximum possible speed of 30 m/s. At any instant, the entire area within the envelop will be filled with particles capable of harming the person. Try to obtain the equation of the envelop at any instant t. And that will solve the problem.
@kaymant sir
differentiating equation of trajectory i got -
\large y_{max}\leq \frac{u^{2}}{2g}\,- \frac{g x^{2}}{2 u^{2}}
sir is this the required envelop u hinted about???
putting u = 30, x= 30, g=10
\large y_{max}\leq 40
now acc. to question
u is less than or equal to 30 m/s
for the range = 30m
let ny peice of bomb gone making angle * with horizontal
now R= u^2sin2*/g
now u<30m/sec
R< 30 . 30 . sin2*/9.8
putting R= 30
sin2* > 9.8/30 = 1/3.2
cos^2 2*> 1- sin^2 2*= 1- 1/10 = 9/10
cos2*= + or - 3/root 10
now cos2*= 1-2sin^2*
put one time - nd then +
+ will be neglected
Using minus u will get the value of sin*
now put it in the eqn T= 2 u sin*/g
after solving u will get T< 5 sec (app.)