1forgot . It performs pure rolling
Discuss the various possibilities for differetn ranges of v0 . velocity is parallel to AB
case(i) - when it passes from AB to BC smoothly i.e. along the surface .
case-(ii) - when it loses contact at B.
case(iii)- when it moves up a certain distance and then comes down. back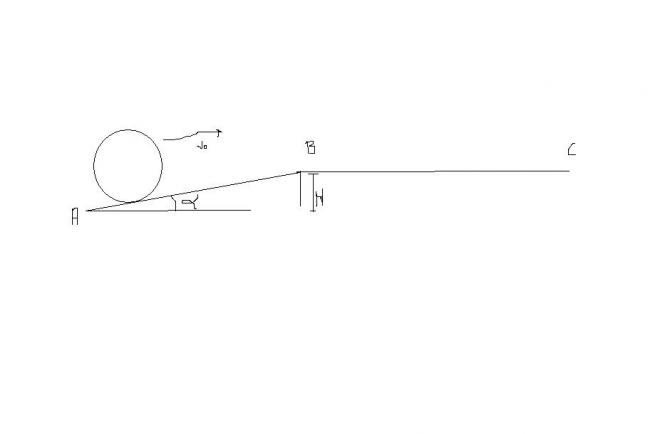
-
UP 0 DOWN 0 0 8
8 Answers
62Hint:
Everything changes with the normal reaction of the ball. at that point!
The third part is easier.. you have to use energy so that the ball does not become horizontal
1the normal reaction is in between as u said . this must be the daigram . with Mg is this fine?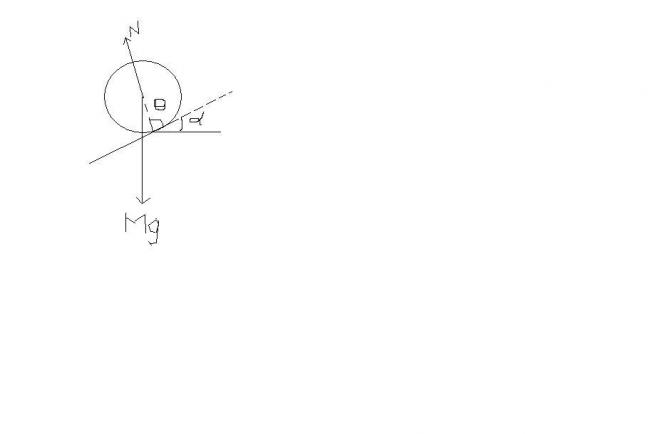
1add a frictional force as well, parallel to AB and acting A→B... this doesn't do any work though but is required for pure rolling!!
1part I) firstly balance the force . condition is N>0...
then apply energy conservation abt B. find reqd. ω..
N + mω2R = mgcosα
for N>0 , ω2 < gcosα/R
about B,
1/2Iw02-1/2Iw2 = mgR(1-cosα)
take care of inequality sign and find out w0 from here.
then v0 = w0R (:P ... as if yeh bhi kisika doubt ho sakta hai :P)
part II ) jus put N=0.
part III) 1/2mv2 + 1/2Iw02 = mgH
actually this will give uu the w0 for the body to reach jus till B.
to get the exact value of w0 we need the 'certain distance' that it moves up.. then we replace H for that value of height.
1hey boss u just have missed out friction forces i.e rolling friction which will be acting upward through thr is no relative motion at the point of contact but due to component of force parallel to Surface thr is tendency to fall down so rolling frictional force will act upward here