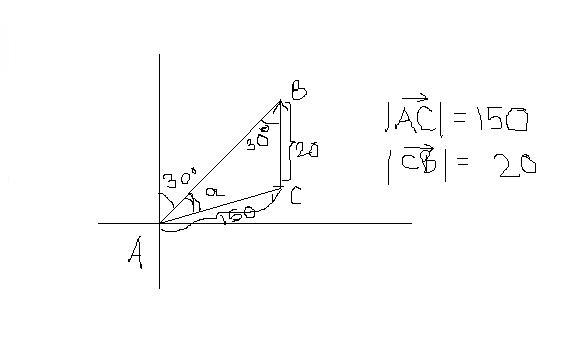
My solution
AB2=(√Vaw2+Vw2+2VawVwcosα)2
We then find α from here and get the angle.
But my ans is not matching the the ans of the book.
Cud u please correct me.....
An aeroplane has to go from a point A to another point B,500 km away due 30° east of north .wind blowing due north at as speed of 20m/s.The air-speed of the plane is 150m/s.(a)Find the direction in which the pilot should head the plane to reach point B.(b)Find time taken by the plane to go from A to B.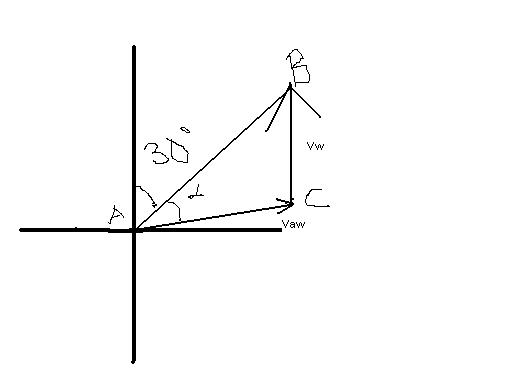
-
UP 0 DOWN 0 0 10

10 Answers
kalyan,i think the angle a can be easily found out.
in the triangle ABC.
a/sin A = b/sin B
here B=30°,a=20,b=150
A=sin-1 (1/15)
now using resultant velocity formula as u used above get the resultant velocity and time taken will be 500000/resultany velocity.
yeah dis was the solution given in arihant..bt wat is wrong if i use d method shwon above???
kalyan there are 2 variables in ur equation:angle a and vel of the plane in still air.
first find a and then solve for the 2nd part.
btw i hope u dint confuse AB vector with position vector or sumthin.had probably dun this earlier in verma.
but arka da vel of plane is given
see:
The air-speed of the plane is 150m/s
eta hi toh??
if not then wat is it??
but boss u dont kno about AB
AB n Vab r not same bhalo kore dak ur equating velocity wit distance!!!!
maha paap
a nice way to prevent such blunders is dimensional analysis....
devote time to tis topic .....sometimes u may eliminate 1,2 or even 3 of the four choices [5]
yes kalyan thats AC vector.
AB vector is not known and neither is angle a.
thats why u need the 2 equations.
AB2=Vaw2+Vw2+2VawVwcosα ..1
and a/sin A = b/sin B ...2.