[1]
Can somebody mathematically prove that at resonance, amplitude of the oscillating system becomes high?
This might be simple but most of us only know the fact and don't have this proof. Try it..
-
UP 0 DOWN 0 1 12

12 Answers
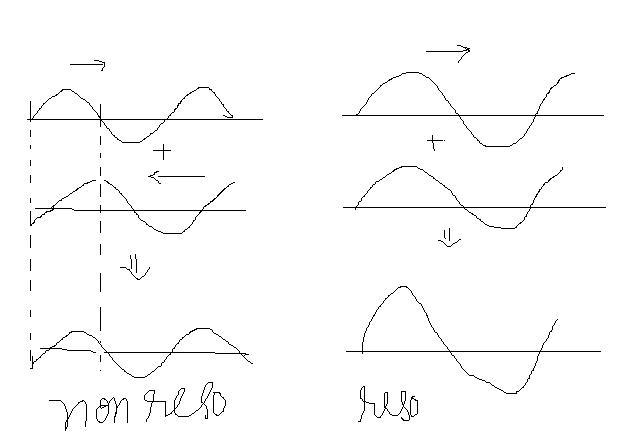
max for wave from both side at same point so A is max...
in other condition maxima is not at same point...
Anyone else who wanna give a try......
that was a very good try priyam........
but how to prove mathematically....not graphically
its just that at resonanse waves interfere constructively at all places
@celestine..... The thing u r saying is true for transverse waves.
Prove this for longitudinal waves just like the oscillations of a mass connected to a spring..
Guys here is the way I solved it.
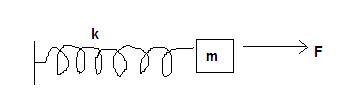
consider the oscillation of a spring having mass m.
let a force F = F0cosωt is applied to the system.
therfore:-
ma = -kx + F0cosωt
x" " + (k/m)x = F0cosωt / m ......... (1) ( x" " denotes double differentiation of x)
At the steady state where the system begins to oscillate with the frequency of the force other than its natural frequency.
x = Acosωt where a = amplitude
→ x" " = -Aω2cosωt
Putting this in (1), we've
-Aω2cosωt + (k/m)Acosωt = F0cosωt / m
→ A (k/m - ω2) = F0 / m .............(2)
Now the natural frequency of the system is given by
ωo = √ (k/m)
putting in (2) :-
A = (F0 / m) / ( ωo - ω2) .......... (3)
From equation 3:-
If ω = ωo
denominator becomes 0 and A → ∞.
This is resonance.
Further cases arises if ω <<<<< ωo
then A → Fo / k
and if ω >>>>> ωo or simply when ω → ∞ , A → 0.
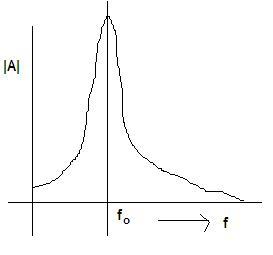
hence if the graph is plotted between A and f (f = 2πω) we have the following graph:-