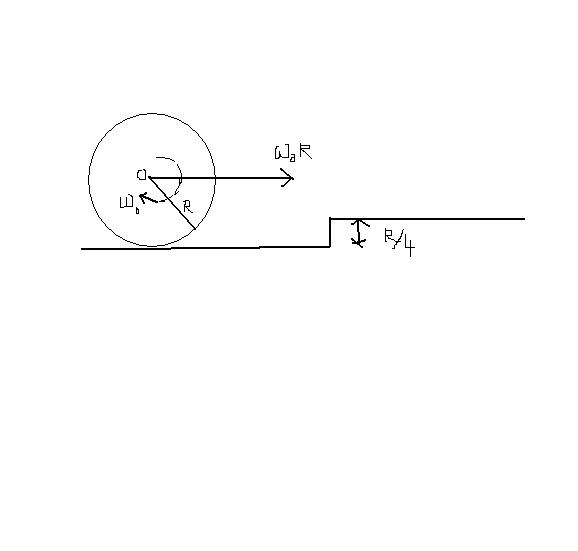
a cylinder of mass 'm' and radius 'r' is rolling widout slipping on a horizontal surface wid angular velocity ω0. the velocity of center of mass of cylinder is ω0r. the cylinder comes across a step of height r/4. (assume required friction is present at the edge of the step.) answer the following questions based on above info.
1.) the angular velocity of cylinder just afetr the collision is
(assume cylinder remains in contact and no slipping occurs
on the edge of the step)
a> 5ω0/6
b> ω0
c> 2ω0/3
d> 6ω0/5
2.) find the minimum angular velocity (ω0) of cylinder so that the cylinder rides up the step without slipping or jumping
a> 2/5 √(3g/r)
b> 3/5 √(3g/r)
c> 5/2 √(3g/r)
d> √g/3r
3.)the maximum angular velocity (ω0) of cylinder so dat the cylinder rises up the step without slipping or jumping
a> 2/5 √(3g/r)
b> 3/5 √(3g/r)
c> 5/2 √(3g/r)
d> 1/2 √(3g/r)
-
UP 0 DOWN 0 1 8

8 Answers
I will solve the first part.. and leave the rest as attempts for u...
if u cant get them.. post again....
First.. angular momentum about the tip of the stair before contact
= mv(r×3/4) + Iω (I is about the CM)
I=mR2/2
Just after colission it will start pure rolling about the point of the stair..
Ip = I + mr2
now balance angular momentum at both the points! I guess this is sufficient :)
yup.....thank you....
got the second part.......
1/2Iω2 + 1/2 m(ωr)2 = mgr/4
plz give a hint abt the last part.... wen it will be max.?
One traditional method can be by impulse method...... but i m trying it with some other......
Oh my god i have just lost hold over the topic!!!!
Have to just work on rot .....
Oh finally got it....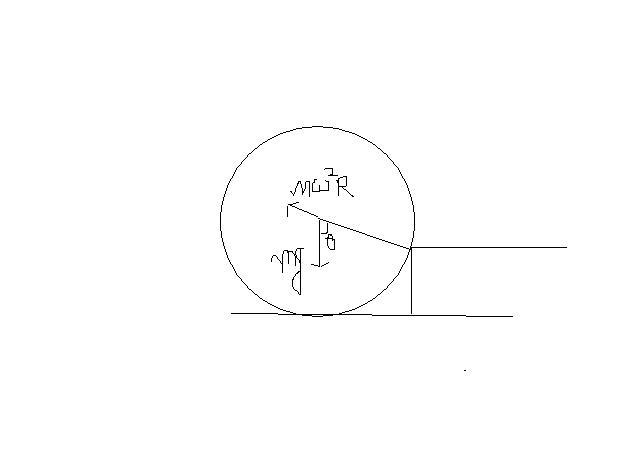
mg cosθ=mω2R
cosθ=3/4
ω=(3g/4R)1/2
ω0=6ω/5 frm Q.1
ω=3/5√(3g/R)