1YAAR PLEASSE KOI TO KAR DO......
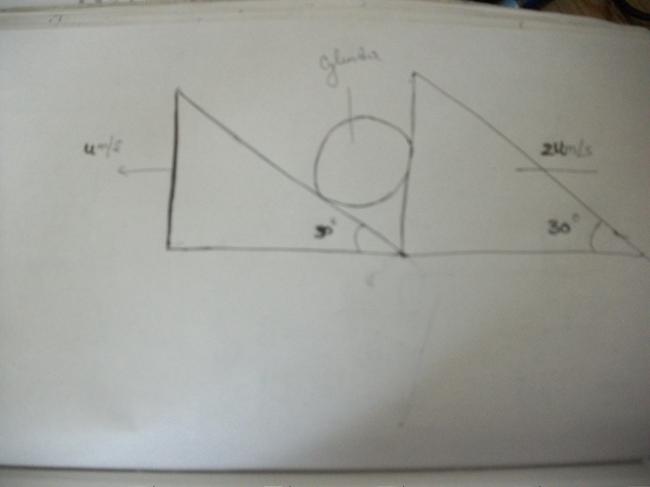
A thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment the end B starts experiencing a constant force F which is always perpendicular to the original posn. of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle 'x' counted relative to the initial position...
ANS GIVEN IS ...... √(6F sin xml)
-
UP 0 DOWN 0 0 8
8 Answers
1hint:
use Eqn
\large \tau\, d \theta = (Iw )\: dw
where \large \tau is torque acting on rod due force
&
\large \omega is angular velocity
1system is shown in the figure.assume that cylinder remains in contact with the two wedge.the speed of the cylinder is.angle of both the wedges r 30 degree and the left wedge is moving with a speed u to the left and the right one with a speed 2u to the right. 
1hey harsh i couldn't get u.what r u trying to explain.as a constant force is acting on the point b but is always in the direction perpendicular to its initial position.i couldn't get that statement even would u plz explain me once
1@Manmay.........
4 ur Q.......
wat I got was √(6Fxcosx)/(ML)
Γ=FLcosx=Iα=Ml2α/3
or α=3Fcosx/ML
ω=√2αx = √(6Fxcosx)/(ML)
Could U lemme noe wats wrong[7][7][7]
