Rotation (relative angular speed)

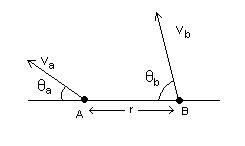
Are the particles undergoing circular motion?

rotation

yes aragorn whn u r in the frame of reference of A or B the other particle will seems to rotate

priyam, i think ur ans is right...this was one of the options given..
but hw did u do it??

similoar case..

jus here u have the vel at some angle...

[remember.... v = r X ω ... thats y we will take the perpendicular component ]

See...

As velocity (as told beautifully by Sky above (hehehe up above there is sky only :P)) is cross product of r and ω so we only care for velocity perpendicular to r (as it perpendicular velocity is product of ω and r) so only perpendicular component of velocity is shown in teh figure below:

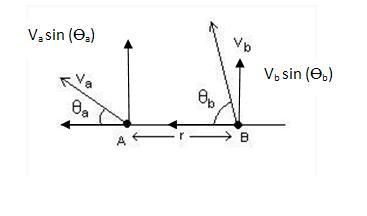
as A is the observer so he (she) sees himself (herself) at rest and adds his (her) negative velocity to other particle (here B)..

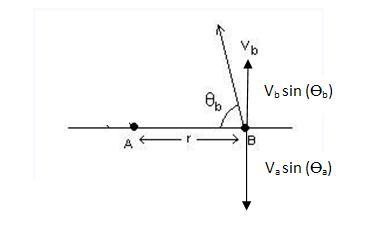
so now wrt A velocity (perpendicular to the distance i.e. r) of B is

(v_bsin(θ_b)-v_asin(θ_a)

so (as it is clear from the elegant example by sky above )
ω is (v_bsin(θ_b)-v_asin(θ_a)
r

Note: don't consider it as division or cross division of vectors..
:P
Just kiddin..
[1]

thanx, Sky and Priyam....[:)]