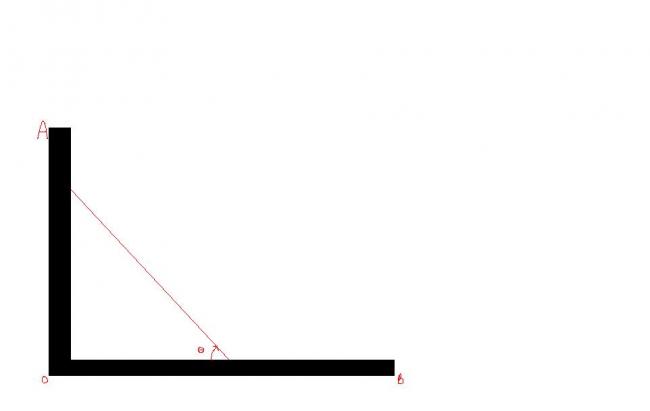
a uniform bar of length L stands vertically touching a wall OA, when slightly displaced, its lower end begins to slide along the floor . obtain an expression for the angular velocity ω of the bar as a function of θ
1yahi question tha jo ith power ne solve kiya tha...
and wats the ans for your prev question ?
11
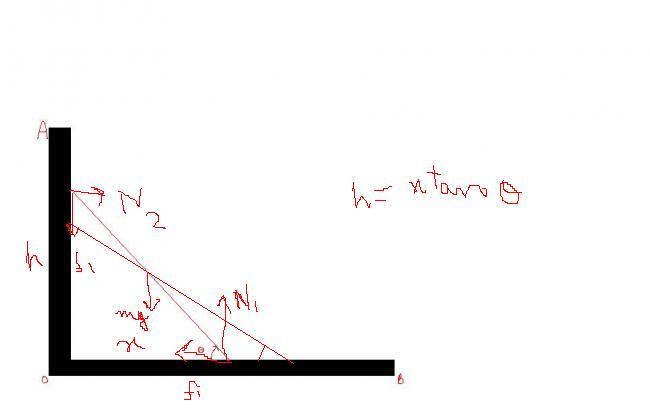
EQUATIONS TO BE USED
1)NET TORQUE ABOUT COM IS 0
2)RESOLVE THE FORCES IN THE VERTICAL DIRECTION
3)RESOLVE THE FORCES IN THE HORIZONTAL DIRECTION
4)LOSS IN P.E =GAIN IN K.E+GAIN IN ROTATIONAL ENERGY
3see its force to move along the walls[ends of the rod refers to it]
so IC is as shown in figure .......
mgl/2[1-sinθ] = 1/2 I(IC) W2 .......(1)
I(IC) = ml2/12 + [ml2cot2θ]/4 ............(2)
solve for w frm eqxn 1 ,2 .........
ull get w = √12g(1-sinθ)/(1+3cot2θ)L
11have a look at it
http://en.wikipedia.org/wiki/Instantaneous_axis_of_rotation
