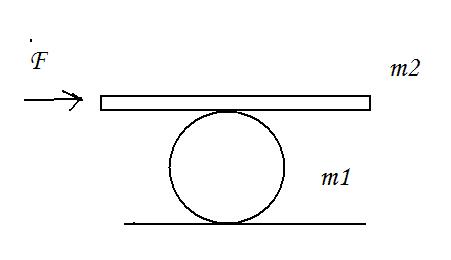a man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown. There is no slipping at any contact. The horizontal component of the force applied by the man is F. find:
(a) the accelerations of the plank and the centre of mass of the cylinder, and
(b) magnitudes and directions of frictional forces at contact points.
1
F - f1 = m2a1 .........................(1)
f1 - f2 = m1a2..........................(2)
Iα = (f1+f2)R
→ α = (f1+f2)R12m1R2.........................(3)
a2 = Rα ....................................(4)
and a1 = a2 + Rα........................(5)
solving abv equations we get
a2 = 4F3m1+8m2
f1 = 3MF3m1+8m2
f2 = MF3m1+8m2