A steel ball of radius R=20cm and maass =2kg is rotating about a horizontal diameter with angular velocity w naught=50 rad/sec. this rotating ball is dropped onto a rough horizontal floor and falls freely through a height of h=1.25 m. the coefficient of restitution is e=1.0 and coefficient of friction between ball and the floor is mu=0.3. calculate (1)distance between points of first and second impact of the ball with the floor. (2)loss of energy due to friction (g=10m/s^2)
pls try and give me a detailed sol.
-
UP 0 DOWN 0 0 4

4 Answers
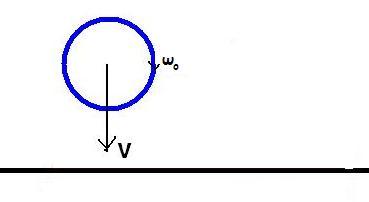
let the ball fall on the floor with final velocity (-v).
e=velocity of recoilvelocity of approach=1
so,velocity of recoil=velocity of approach
so in vertical direction,
velocity of recoil = v
now let impulsive normal reaction N act during collision,
thus Ndt=change in momentum=mv-(-mv)=2mv....(i)
now there wud be impulsive friction acting on the sphere due to impulsive normal reaction,
f=μN.
(Impulsive torque).dt=change in angular momentum=Iω-Iωo
or, μNRdt=Iω-Iωo
or, Iω=μNRdt+Iωo
now impulsive impulse will give horizontal impulse..
so, μNdt=mvhorizontal
or, μ(2mv)=mvhorizontal [from (i)]
or, vhorizontal=2μv
now there will be projectile motion in which
vy=v
and vx=2μv
so the range of this projectile will give us the distance between points of first and second impact of the ball with the floor.
and for part two we will have to do this
the energy in vertical direction is conserved....
so loss in energy=12Iωo2-12Iω2+12m(2μv)2-
the answer will be thus achieved!!![1][1][1]
can anyone give a gym-ed solution???
my solution is just so MOTA!!![2][2]
i am asking for a slimmer solution!! nishant bhaiya can u help?