Won't the time contain the length L of the plank.
And ball is a solid sphere.
Two balls of equal density, and radii r and R =2r, are placed with the center of the larger one at the middle of a cart of mass M and length L. The mass of the smaller ball is m. The balls are made to roll, without slipping, in such a way that the straight line joining their centers remain at a constant angle \varphi to the horizontal. The cart is pulled with a horizontal force (the arrow shown to the right). (i) Find the force with which the cart is being pulled. (ii) How much time elapses before the balls fall off the cart.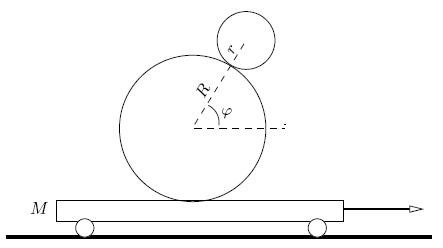
-
UP 0 DOWN 0 0 9

9 Answers
well then i am not getting a good looking answer for the first one ...
let me post the answer to the second one
if it is correct then i will post the first too :)
the answer i got for the second :
√(18(1+sinφ)/(5gcosφ))
i am very sorry that was a typo ..
it will be
√(18L(1+sinφ)/(5gcosφ))
okay heres my solution ...
let the friction force f1 act to the lower plank Backwards ..
we get
(F-f1)/M=a
forces on 8m =
i) f1 forwards
ii) N due to upper mass m at angle of φ to the horizontal bakwards
iii)f2 due to the upper mass m at an angle φ to the vertical anticlockwise
iv)8mg downwards
v)N2 upwards
acceleration of lowermost point due to torque due to both frictions
(f1+f2)R=2(8m)R2/5 (α)
gives
αR=5(f1+f2)/16m to the right
further total acceleration of contact point below=rotational + translational
let net translational acceleration of 8m be to the right
net force to the right ..
f1-f2sinφ-Ncosφ
so contribution of translational acceleeration =
(f1-f2sinφ-Ncosφ)/8m = dv/dt -----(iii)
v=velocity of 8m to the right at ans instant
hence we get
as there is no slipping
(F-f1)/M = (f1-f2sinφ-Ncosφ)/8m + 5(f1+f2)/16m -- (i)
further
as the mass m remains at a constant angle φ w.rt horizontal ..
w.r.t 8m its velocity is zero ..
hence velocity of m towards right is also v
forces acting on m
i)N at an angle of φ to the horizontal to the right .
ii)f2 at angle of 90-φ to the horizontal clockwise to the right .
iii)mg downwards
further as m is not moving vertically net force =0 along vertical ..
hence
Nsinφ=mg+(f2)cosφ ------- -- -- - (A)
further as mass of m is also v
mdv/dt=Ncosφ+(f2)sinφ ---- (ii)
further as the mass m remains at the position w.r.t 8m
there should be no slipping at their point of contact .
hence
taking w1 and w2 to be anti and clockwise respectively .
w1R=w2r
2w1=w2
thus 2dw1=dw2
further writing equations of torque on both
(f1+f2)R=2(8m)R2/5 * dw1/dt
and for m
-f2r=2mr2/5 (dw2/dt)
dividing both we get
2(f1+f2)/(-f2) = 8*4*1/2
thus
f1+f2=-8f2
f1+9f2=0
dividing (ii) and (iii) we get another relation between f1 and f2 and N
f1=9(f2sinφ + Ncosφ)
further from (A) we have
Nsinφ=mg+(f2)cosφ
eliminating f1 f2 and N from these thre equations we get
all three and thus we get all the answers
further at the
satan, its pretty straining to read your solution. However, you must have some mistake somewhere because, the expression for the time (i.e. the second answer) is slightly off-track. Let me the give the answers and may be you can find your mistake:
(i) F = \left(9m + \dfrac{7}{2}M\right)\dfrac{\cos\varphi}{1+\sin\varphi}
(ii) t=\sqrt{\dfrac{2L}{5}\cdot \dfrac{1+\sin \varphi}{\cos \varphi}}
oooooopsss
wrote 9(f2cos2φ/sinφ + mgcotφ)
= 9f2cos2φ/sinφ + mgcotφ
!!!
yes i was missing a factor of 9 in f1's value
now i have got it right 18/9=2 . .....
so let me post the rest of the answer ..
f1 +9f2=0 already obtained ..
further we get
f1=9(f2sinφ+Ncosφ) in my previous post
and Nsinφ=mg+f2cosφ that tooo in my prev post .
we get
f1=9f2sinφ+ 9Ncosφ
=-f1sinφ + 9(f2cos2φ/sinφ + mgcotφ)
=-f1sinφ + 9f2cos2φ/sinφ + 9mgcotφ (here was my mistake :(((()
thus
f1=-f1sinφ -f1cos2φ/sinφ +9mgcotφ
thus f1=-f1/sinφ +9mgcotφ
thus
f1=9mgcosφ/(1+sinφ)
this will give all the answers :)