1Question 2... Let it be xth step. Then it travels x m along x-axis,and x m vertically downwards. x=10t..(1) x=1/2*gt2....(2) solving we get t=2,,and (x=20 Ans)
It's pretty well known that physics is my weak point...so I hope people wouldn't mind if I needed help in some basic problems.
Besides, this isn't my homework either :P...been there done that LOL.
Q1. Three links are hinged together to form a triangle BAC(B the top vertex, A the left one and C the right). We are given that -:
Angle BAC = 45°
Angle BCA = 60°
At a certain instant, the point A is moving towards the mid-point of BC with a velocity 5 m/s and B is moving in a direction perpendicular to AC(magnitude not given). The velocity of point C is?
Q2. A ball rolls off the top of a step ladder with a horizontal velocity of 10 m/s. If the steps are 1m high and 1m wide, the ball will hit which step?
a) 3rd
b) 20th
c) 12th
d) 10th
Q3.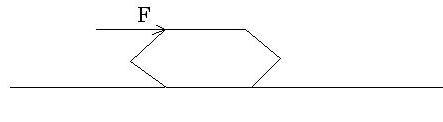 
For the toppling of a regular hexagon, the coefficient of friction must be
a) > 0.21
b) < 0.21
c) = 0.21
d) ≤ 0.21
The force is being applied on the top-most side of the hexagon.
How did 0.21 come into the picture at all?
Q4.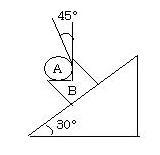 
A cylinder of mass m rests in a carriage as shown. Calculate the maximum acceleration of the carriage so that the cylinder does not loose contact at B(nothing about friction given).
-
UP 0 DOWN 0 1 2
2 Answers
1
39Text Erased
First, making an FBD of forces acting, we find that :
Force F acts on the topmost side parallel to it.
Force mg acts downwards from the centre of gravity of the hexagon.
Force Fr(friction) acts on the base of the hexagon, opposing the impending motion(opposite in direction to F).
Also, we know that F = μmg.
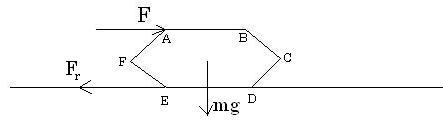
As the block is to topple, the rotational axis passes through point D and is perpendicular to the plane of the hexagon.
We then have to find the torques due to the various forces.
Let the hexagon have side "a".
Torque Due to F
In triangle BCD, by the cosine rule,
cos120° = a² + a² - BD²2a²
=> BD = √3a
Ï„F = F * √3a, as √3a is the perpendicular distance of the line of force F from the axis of rotation.
Torque due to weight
Clearly, we see that from the line of force mg, the axis of rotation is at half the distance ED, which is a/2.
So Ï„mg = mga2
Torque due to friction
The line of force of friction intersects the axis of rotation, hence there is no torque due to it.
Clearly we see that force F provides a clockwise torque and force mg provides an anticlockwise torque.
For toppling,
Ï„F > Ï„mg
=> √3aF > mga2
=> √3 * μmg > mg2
=> μ > 0.28 > 0.21
Hence (A) is the answer.