A uniform rod length L and mass m2 is pivoted at one end, to its other end is fastened a uniform disk of mass m1 and radius b. Find the angular acceleration of the system just after it is released from the position shown.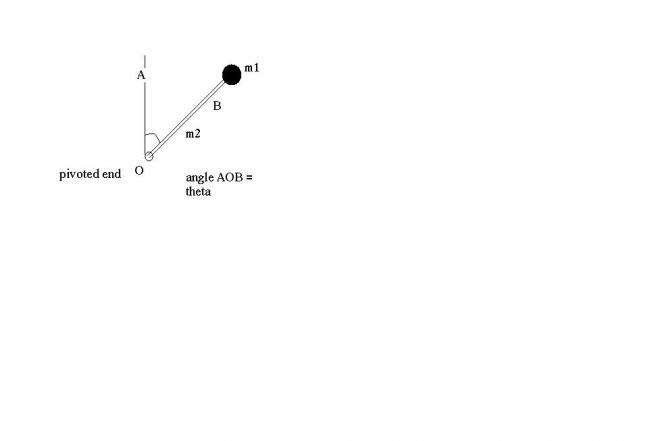
1torque= m2gL/2cosθ+m1gLcosθ
moment of inertia abt O=m2L2/3+m1b2/2+m1L2
now angular acceleration=torque/I
1ok
there will be two torques
one due to m1 and other due to m2
hence the expression
and moment of inertia of rod=moment of inertia abt com+M(L/2)2
=ML2/12+ML2/4=ML2/3
and for the disc
moment of inertia = moment of inertia about of com of disc +M(L)2
Mb2/2+ML2
39m2gl/2cosθ is the torque due to the weight of the rod.
m1glcosθ is the torque due to the mass m1.
m2l2/3 is the moment of inertia of the rod aout an axis passing through the end and perpendicular to it.
m1b2+m1l2 is moment of inertia at o due to the disc [from parallel axis theorem]
now angular acceleration= torque/I
1please explain how u hve calculated torque [ f.r where r =perpendicular dist. from the axis of rotation]
62yeah that is how shreya..
there are 2 parts of the problem..
one is the point mass..
the other is the rod...
U need to consider both of these!
If it is still nto clear do ask..
1please solve the whole problem i am not able to cal. the torque
how did u find r
62
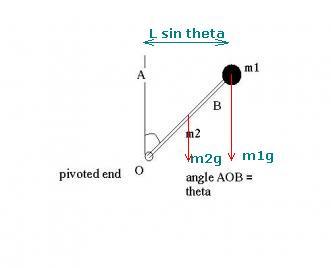
Torque due to m1 will be : m1gLSinθ
due to m2 will be : m2gL/2 Sinθ
As rohan wrote!
and moment of inertia of rod=moment of inertia abt com+M(L/2)2
=ML2/12+ML2/4=ML2/3
and for the disc
moment of inertia = moment of inertia about of com of disc +M(L)2
Mb2/2+ML2