1actuaaly i donn know the ans...so i cant tell anything....buh i think its right
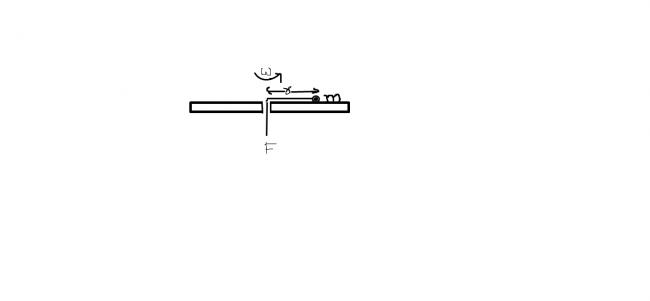a small partical of mass m n its restraining cord r spinning with an angular velocity ω on the horizontal surface of a smooth disc as shown..the force F is slightly relaxed , r increases n ω changes. 1.∂ω/∂r=-ω/r 2.∂ω/∂r=-2ω/r 3.∂ω/∂r=ω/r 4.∂ω/∂r=2ω/r
-
UP 0 DOWN 0 0 3
3 Answers
62i think what you mean is F=mω2r
mass is constant and
∂F=m2ω∂ωr + m ω2 ∂r
since the force is not changed.. It is relaxed and brought back.. if i understood it correctly!
m2ω∂ωr + m ω2 ∂r =0
∂ω/∂r = - ω/2r
doesnt seem like i am getting anything good! :(
1
66The angular momentum about the center of the circle must remain constant. So that
\omega^2r=\textrm{ constant}
Taking differentials, we get
2r\omega \ \mathrm{d}\omega + \omega^2 \ \mathrm{d}r=0
which gives
\dfrac{\mathrm{d}\omega }{\mathrm{d}r}=-\dfrac{\omega}{2r}