1first of all think about the situation after the strings break
calculate the KE then.
and after the two strings become taut again find the new KE
thus find the fractional loss in KE.
That is it. Nothing too complex.
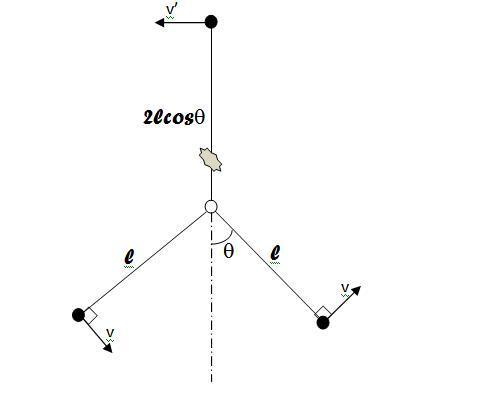
A setup consistomg of 3 identical balls (points) attached to a small massless ring is rotating on a smooth table.
it is known that the ring is at rest at the instant shown in the figure.
Just now however one of the strings break.
when the intact strings become taut again find the fractional loss of kinetic energy of the system.
For what θ is this loss maximum?
P.S. the setup is symmetrical about the dashed line and assume the collision to be plastic
-
UP 0 DOWN 0 2 15
15 Answers
11maybe like you did here
http://targetiit.com/iit-jee-forum/posts/impulse-momentum-12208.html
1bhaiya i am getting energy of the system after string becomes tight as
mv2(3+Cos2 2θ)4
is it correct ?
1looks like you're really close.
check your calculations once again and post the fractional loss in KE that you get.
Im asking for fractional loss because the expression will be simpler and also independent of m and v
1no.
post your working if you can or the general method.
Its hard to spot the mistake like this.
1bhaiya i have considered all three balls as my system .
i found the velocity of the upper particle v' by finding the tension considering circular motion and assuming T to be the tension in the lower string to find tension in the upper string.
after the upper string snaps we observe that both lower have same horizontal velocities but opposite vertical velocities.
when string is about to become taut . i resolved the velocities of the particles perpendicular and along the string .
After collision component of the velocities perpendicular to the sting will remain unchanged.
velocities of the balls along the string will become equal .
conserved momentum along the strnig.
now i found ΔKk
bhaiya i recheked my calculations again i am sorry! is the answer
2(cos2θ-1)1+Cos2θ
1did you not notice that your answer is always <=0 ?
its wrong. :(
method looks ok
can you show the situation of the string just b4 it becomes taut ?
1ok I will post it.(though i dont see how the answer is gonna help)
Its inexplicable why most of the you are ignoring this one.
cause i think this is well within JEE level if not below.
1Ok definitely people think this is too easy so I'm posting the soln:
A second look at the problem will tell that the ring is place on the CoM of the system also is given that it is at rest
so v' comes out to be 2vcosθ
it should be clear that if now the string breaks, the top mass m will continue to move in a straight line with v'
However now the two strings left are no longer taut.
so the two masses continue to move with their respective velocities in the direction shown until the separation b/w them is 2l...
The situation just b4 the strings are taut will be like this....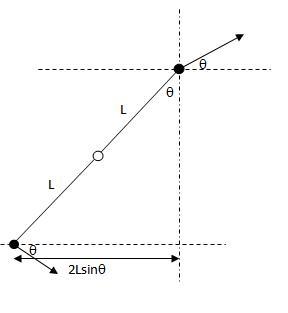
now we only need to find the change in energy so we may just tilt our heads a little to make it like this :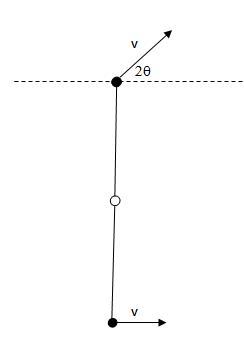
now it all materializes as extremely simple....
the velocities in the upward direction will distribute among both impartially and the horizontal directions will remain unaffected...
so the final KE of the 3 masses will be
K_f=\frac{1}{2}m\left((2vcos\theta )^2+ 2(\frac{vsin2\theta}{2} )^2+(vcos2\theta )^2+v^2\right)
hence\ \Delta K=\frac{1}{2}m.\frac{(vsin2\theta)^2 }{2}
1one doubt philip :
how u arrived at the geometry of the situation just b4 getting taut
1oh sorry for not mentioning , I thought that was obvious..
the horizontal component of separation remains 2lsinθ always upto that instant and the separation just b4 the string get taut will be 2l so everything follows..
btw if you had put this on paper even once u would've understood i think