Subhomoy is having the right answer.Would you like to show me your working?
A thin unifor rod is suspended in vertical plane as a physical pendulum about point A.The time period of oscillation is T0.Not counting the point A,the number N of other points of suspension on rod such that the time period of oscillation(in vertical plane) is again T0.Then the value of n is:(Since the rod is thin,consider one point for each transverse cross section of the rod)
(A)0 (B)1 (C)2 (D)3
-
UP 0 DOWN 0 0 11

11 Answers
I am having a feeling like this.I have been told by many persons to speak like this.Including my teacher,Mr.Manish Verma(I.I.T. Madras),who taught me I.I.T.
I am so stupid because I did not concentrate on studies while he was teaching.
Hey Kunl,If you have to talk about stupidity of me,then please give your email and take mine.We will talk too much on that matter.This forum is meant to discuss about IIT topics only(just jee).Not for other matters.I think I am the moderator here and Nishan sir is a user.That's what I think?
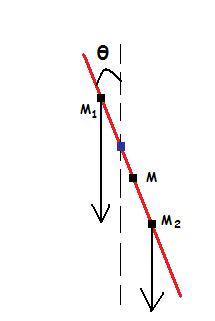
M is the COM of the thin rod i.e. at midpoint!
The rod is hinged at a point at distance (l) from the one end.
Thus the length of other segment is (L-l).
the upper part in the figure provides anticlockwise torque and the downward part provides clockwise torque..the system will be in stable equilibrium i.e. perform angular periodic motion if and only if clockwise torque is more than anticlockwise torque.
anticlockwise torque = \left( l.\lambda \right).g.\left(\frac{l}{2} \right)sin\theta
clockwise torque = \left[ \left(L-l \right).\lambda \right].g.\left[\frac{L-l}{2} \right]sin\theta
net magnitude of torque = \left[ \left(L-l \right).\lambda \right].g.\left[\frac{L-l}{2} \right]sin\theta - \left[l.\lambda \right].g.\left[\frac{l}{2} \right]sin\theta=\frac{\lambda gsin\theta }{2}\left[\left(L-l \right)^{2}-l^2 \right]=\frac{\lambda gsin\theta }{2}\left[L^2-2Ll \right]={mgsin\theta }{}\left(\frac{L}{2}-l \right)
so, \tau = {mgsin\theta }{}\left(\frac{L}{2}-l \right) = K - mglsin\theta
and this will have a specific time period.!
This time period is dependent only on the non-constant part i.e. part devoid of L
Thus for another l , (L2 - l) must be equal to -l ! and it will also have same time period!
Now same time period will be achieved if we take the respective distances of l from the other end too!
So in all we have 4 points on the rod giving the same time period of oscillation!
Out of these four points we have one as A.
Thus three more points exist which will give the same time period of oscillation as that of A.
Hence, n=3
Just a little trivia - The time period of pendulum remains constant for the point of suspension as well as the center of oscillation , as well as the images of these points on the other side . So , the required number of points is 3 .